2020 전산통계학 6차 과제 (마지막) - F, T(paired), Sign, kruskal, lm

1번) 강의자료에 설명된 알고리즘들을 사용하여 R의 var.test (F test) 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

# (var)F test to compare two variances

x <- c(91.50, 94.18, 92.18, 95.39, 91.79, 89.07, 94.72, 89.21)

y <- c(89.19, 90.95, 90.46, 93.21, 97.19, 97.04, 91.07, 92.75)

 

# make f.t

var.t <- function(x1, x2, alpha) {
n1 <- length(x1) ; n2 <- length(x2)
s1 <- var(x1) ; s2 <- var(x2)
fstar <- ( s1/ s2 )
half<- qf(0.5, n1-1, n2-1)
cl <- 1-alpha
 
if(fstar < half) {fpvalue <-2*(pf(fstar, n1-1, n2-1))}
 else {fpvalue <-(2*(pf(fstar, n1-1, n2-1, lower.tail = F)))}

ub <- (s1/s2) / qf(cl/2, n1-1, n2-1)
lb <- (s1/s2) / qf(1-(cl/2), n1-1, n2-1)

# make sentence equal to var.test (in R)
cat("\n F test to compare two variances\n\ndata: x and y
\nF = " ,round(fstar,5),", num df = ",n1-1 ,", denom df = ",n2-1 ,", p-value = ",round(fpvalue,4)
, "\nalternative hypothesis: true ratio of variances is not equal to 1" ,"\n"
, (alpha)*100 , " percent confidence interval:\n ", lb," ",ub, "\n", "sample estimates:
\nratio of variances \n", " ", fstar, sep = "")
}

# campare my f.t with original f.t (in R)
var.t(x,y, .9) ; var.test(x,y, conf.level = .9)

---

2번) 강의자료에 설명된 알고리즘들을 사용하여 R의 T test(var.equal & paired data) 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

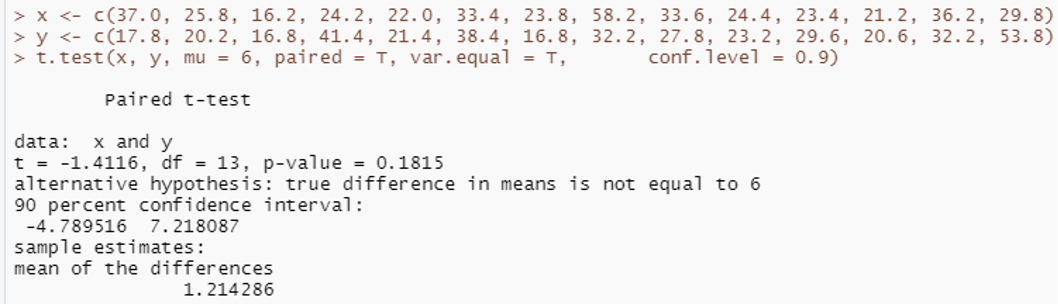
# Paired t-test
x <- c(37.0, 25.8, 16.2, 24.2, 22.0, 33.4, 23.8, 58.2, 33.6, 24.4, 23.4, 21.2, 36.2, 29.8)
y <- c(17.8, 20.2, 16.8, 41.4, 21.4, 38.4, 16.8, 32.2, 27.8, 23.2, 29.6, 20.6, 32.2, 53.8)

# make f.t
t.tve <- function(x,y,mu,sided,alpha) {
d=(x-y)
n<-length(d)
Sd<-sqrt(var(d))
tstar<-(mean(d)-mu) / (Sd/sqrt(n))
df<-(n-1)

if(sided=="two.sided") {
ifelse(tstar > 0 , bf.pvalue<-pt(tstar,df,lower.tail = F)*2, bf.pvalue<-pt(tstar,df)*2)
pvalue<- round(bf.pvalue,7)
result <- c("alternative hypothesis: true difference in means is not equal to ", mu)
L1<- (mean(d) + qt(0.5-alpha/2, df)*(Sd/sqrt(n) )) ; L2<- (mean(d) + qt(0.5-alpha/2, df, lower.tail = F)*(Sd/sqrt(n) ))
}

if(sided=="less") {
bf.pvalue <- pt(tstar,df)
pvalue<-round(bf.pvalue,7)
result <- c("alternative hypothesis: true difference in means is less than ", mu)
L1<-" -Inf" ; L2<- ( mean(d)+ qt(alpha, df)*(Sd/sqrt(n)) )
}

if(sided=="greater") {
bf.pvalue <- pt(tstar,df, lower.tail = F)
pvalue<-round(bf.pvalue,7)
result <- c("alternative hypothesis: true difference in means is greater than ", mu)
L1<-( mean(d)+ qt(1-alpha, df)*(Sd/sqrt(n) )) ; L2<- " Inf"
}

# make sentence equal to var.test (in R)
cat("\n Paired t-test\n\ndata: x and y \nt = ",round(tstar,4),", df = ",df,", p-value = ",round(pvalue,4)
, "\n",result ,"\n", (alpha)*100 , " percent confidence interval:\n"
, L1," ",L2, "\n", "sample estimates:\nmean of the differences \n", " ",mean(d) , sep = "")
}

# campare my f.t with original f.t (in R)
t.tve(x,y, mu=6, sided = "two.sided", alpha=.9) ; t.test(x, y, mu=6, paired = T, var.equal = T, conf.level = .9)

---

3번) 강의자료에 설명된 알고리즘들을 사용하여 R의 Sign test 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

# One-sample Sign-Test

library(DescTools)

x <- c(35, 65, 48, 40, 70, 50, 58, 36, 47, 41, 49, 39, 34, 33, 31)

# make f.t
s.t <- function(x, mzero, side) {
equal=0 ; low=0 ; high=0
for (i in 1: length(x)) {
if(x[i]==mzero) {equal=equal+1}
else if (x[i]<mzero) {low=low+1}
else {high= high+1} }

qstar.a <- low ; qstar.c <- high
qstar.b <- low+equal ; qstar.d <- high+equal

if (side=="two.sided") {

ah <- c("true median is not equal to ")
if(low<high) {pvalue <- min((1- pbinom(qstar.b-1, length(x),0.5)), pbinom(qstar.b, length(x),0.5))}
else {pvalue <- min((1- pbinom(qstar.a-1, length(x),0.5)), pbinom(qstar.a, length(x),0.5))}
}

if (side=="less") {

ah <- c("true median is less than ")

pvalue <- 1-pbinom(qstar.a - 1, length(x), 0.5)}

else if (side=="greater") {

ah <- c("true median is greater than ")

pvalue <- pbinom(qstar.b , length(x), 0.5)}

if (pvalue>1) {pvalue <- 1}

# make sentence equal to var.test (in R)
cat("\n One-sample Sign-Test\n\ndata: x\nS = ",qstar.c,", number of differences = ",length(which(x!=mzero)),", p-value = ",round(pvalue,4) , "\nalternative hypothesis: true median is not equal to ",mzero ,"\n", "sample estimates:\nmedian of the differences \n", " ",median(x) , sep = "")
}

# campare my f.t with original f.t (in R)
s.t(x, mzero=50, side = "two.sided"); SignTest(x, y=NULL, alternative = "t", mu=50, conf.level = .95)

---

4번) 강의자료에 설명된 알고리즘들을 사용하여 R의 summary (aov) 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

# summary(aov(y~index))
coal <- c(1.51, 1.92, 1.08, 2.04, 2.14, 1.76, 1.17, 1.69, 0.64, 0.90, 1.41, 1.01, 0.84, 1.28, 1.59, 1.56, 1.22, 1.32, 1.39, 1.33, 1.54, 1.04, 2.25, 1.49, 1.30, 0.75, 1.26, 0.69, 0.62, 0.90, 1.20, 0.32, 0.73, 0.80, 0.90, 1.24, 0.82, 0.72, 0.57, 1.18, 0.54, 1.30)
index <- factor(rep(1:5, c(7,8,9,8,10)))
fit <- aov(coal~index)

# make f.t
# Data (y데이터를 리스트화 시켜서 해봄)
y=list()
y[[1]]<-c(1.51, 1.92, 1.08, 2.04, 2.14, 1.76, 1.17)
y[[2]]<-c(1.69, 0.64, 0.90, 1.41, 1.01, 0.84, 1.28, 1.59)
y[[3]]<-c(1.56, 1.22, 1.32, 1.39, 1.33, 1.54, 1.04, 2.25, 1.49)
y[[4]]<-c(1.30, 0.75, 1.26, 0.69, 0.62, 0.90, 1.20, 0.32)
y[[5]]<-c(0.73, 0.80, 0.90, 1.24, 0.82, 0.72, 0.57, 1.18, 0.54, 1.30)

rcd <- function(y) {
k<-length(y)
n<-c()
t<-c()
for (i in 1:k) {
n[i] <- length (y[[i]])
t[i] <- sum(y[[i]])
}
N<-sum(n)
t..<-sum(t)
tn<-c()

# Sum Square
for (i in 1:k) { tn[i]<- sum(t[i]^2/n[i]) }
sstrt<-sum(tn)-(t..^2)/N
yij<-0
for (i in 1:k) { for (j in 1:n[i]) { yij<-yij+(y[[i]][j])^2 } yij }
sstot <- yij-(t..^2)/N
sse <- sstot-sstrt

# Mean Square
mstrt <- sstrt/(k-1)
mse <- sse/(N-k)

# F.star & P-value
fstar <- (mstrt/mse)
pvalue <- pf(fstar, (k-1), (N-k), lower.tail = F)

# ANOVA Table
table <- matrix(c(k-1, N-k, round(sstrt,3), round(sse,3), round(mstrt,4), round(mse,4) ,round(fstar,3), NA, round(pvalue,7), NA) , nrow = 2, ncol = 5, dimnames = list(c("index","Residuals"), c("Df", "Sum Sq", "Mean Sq", "F value", "Pr(>F)")) )
table
}

# campare my f.t with original f.t (in R)
rcd(y) ; summary(fit)

---

5번) 강의자료에 설명된 알고리즘들을 사용하여 R의 kruskal test 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

# kruskal-wallis rank sum test
x <- c(2.9, 3.0, 2.5, 2.6, 3.2) # normal subjects
y <- c(3.8, 2.7, 4.0, 2.4) # with obstructive airway disease
z <- c(2.8, 3.4, 3.7, 2.2, 2.0) # with asbestosis
x <- c(x,y,z)
g <- factor(rep(1:3, c(5,4,5)), labels = c("Normal subjects", "Subjects with obstructive airway disease", "Subjects with asbestosis"))

# make f.t
# Data (y데이터를 리스트화 시켜서 해봄)
y=list()
y[[1]]<-c(1.51, 1.92, 1.08, 2.04, 2.14, 1.76, 1.17)
y[[2]]<-c(1.69, 0.64, 0.90, 1.41, 1.01, 0.84, 1.28, 1.59)
y[[3]]<-c(1.56, 1.22, 1.32, 1.39, 1.33, 1.54, 1.04, 2.25, 1.49)
y[[4]]<-c(1.30, 0.75, 1.26, 0.69, 0.62, 0.90, 1.20, 0.32)
y[[5]]<-c(0.73, 0.80, 0.90, 1.24, 0.82, 0.72, 0.57, 1.18, 0.54, 1.30)

kruskal <- function (x) {
k<-length(x)
n<-c()
t<-c()
y <- rank(unlist(x), ties.method = "average")
M <- c()
for (m in 1:k) { M[m] <- length(x[[m]]) }
x <- list()
for (m in 1:k) { ifelse (m==1, x[[m]] <- c( y[1:M[m]] ),x[[m]] <- c( y[(sum(M[0:(m-1)])+1):sum(M[1:m])] )) }
for (i in 1:k) {
n[i] <- length (x[[i]])
t[i] <- sum(x[[i]])
Ti <- sum (t^2/n)
}
N<-sum(n)

# d.f
hstar <- 12/(N* (N+1)) *Ti -3*(N+1)
pv <- pchisq(hstar, k-1, lower.tail = F)

# make sentence equal to var.test (in R)
cat("\n Kruskal-Wallis rank sum test \ndata: coal by index" ,"\nKruskal-Wallis chi-squared = ",round(hstar,3),", df = ",k-1,", p-value = ",round(pv,7) , sep = "")
}

# campare my f.t with original f.t (in R)
kruskal(y) ; kruskal.test(coal~index)

---

6번) 강의자료에 설명된 알고리즘들을 사용하여 R의 kruskal test 결과인 검정색 글씨부분과 똑같은 결과를 만드는 함수를 만드시오

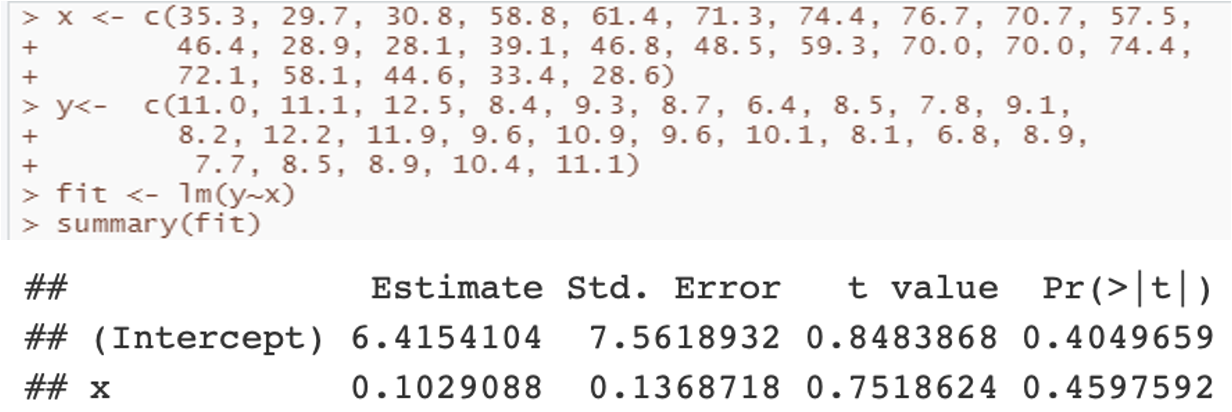
# summary( lm(y~x) ) $ coefficients
x <- c(35.3, 29.7, 30.8, 58.8, 61.4, 71.3, 74.4, 76.7, 70.7, 57.5 , 46.4, 28.9, 28.1, 39.1, 46.8, 48.5, 59.3, 70.0, 70.0, 74.4 , 72.1, 58.1, 44.6, 33.4, 28.6)
y <- c(11.0, 11.1, 12.5, 8.4, 9.3, 8.7, 66.4, 8.5, 7.8, 9.1 , 8.2, 12.2, 11.9, 9.6, 10.9, 9.6, 10.1, 8.1, 6.8, 8.9 , 7.7, 8.5, 8.9, 10.4, 11.1)
fit <- lm(y~x)

# make f.t
lenearm <- function(x,y,x0) {
n <- length(y)
model <- lm(y~x)
df <- (n-2)
sxx=sum((x-mean(x))^2) ; syy=sum((y-mean(y))^2) ; sxy=sum((x-mean(x))*(y-mean(y)))
b1 <- sxy/sxx ; b0 <- mean(y)-b1*mean(x)
sse <- syy-b1*sxy
s <- sqrt(sse/(n-2))
tstar <- abs((b0+b1*x0)/( s*sqrt(1/n+(x0-mean(x))^2/sxx) ))
pv <- pt(tstar, (n-2), lower.tail = F)*2

table <- matrix(c(b0, b1, NA, NA, tstar, NA, pv, NA) , nrow = 2, ncol = 4, dimnames = list(c("(Intercept)","x"), c("Estimate", "Std. Error", "t value", "Pr(>|t|)")) )
table
}

# campare my f.t with original f.t (in R)
lenearm(x,y,x0=0) ; summary(fit)$coefficients

---

<과제 총평>

전체적으로는 해당 두 게시물을 보면 쉽게 해낼 수 있는 과제들 입니다

R, Factorial & Regression program example (15' SCY)

R, Nonparametric test program example (15' LSG & LSM)

 

3번 : equal data (=M0) 는 어떻게 statistic 에 카운트해야 하는지 이 블로그에 3번정도 언급할 정도로 중요하게 인지하고 있어야 함
자세한 것은 해당 게시물을 다시 정독해보자;;;

전산통계학 9차 과제 - 싸인테스트, factorial experiments, 카테고리칼데이터

5번 : 소숫점 아래(예를들어 3~ 자리) 의 미미한 오차정도는 신경쓰지 않아도 됨

 

6번 : 지금은 비록 선형회귀여서 값들이 적지만 다중회귀로 가면 X^n의 계수, 값 들을 구하는 것을 배움 (데이터 분석 시간에 주로 다룸)