미적분학 2-7. 최댓값 및 최솟값

7. 최댓값 및 최솟값

이변수 함수 f(x,y)의 임계점(critical point)를 찾고, 이를 이용하여 극댓점, 극솟점 또는 안장점(saddle point) 등을 이계도함수 판정법을 이용하여 찾는다.

---

예제

f(x,y)="x^4 + y^4 -4xy +1"의 극값과 안장점을 구하여라 

 

with(plots)

f:=(x,y)->x^4+y^4-4*x*y+1

plot3d( f(x,y), x=-2..2, y=-2..2, axes=normal)

fx:=diff(f(x,y), x)

fy:=diff(f(x,y), y)

crip:=solve( {fx, fy}, {x, y})

discr:=diff(f(x,y), x,x)*diff(f(x,y), y,y) - diff(f(x,y), x,y)^2

subs(crip[1], discr)

---

예제

원 "x^2+y^2=1" 상에서 함수 f(x,y)="x^2 +2y^2" 의 극값을 구하여라

 

f:=(x,y)->x^2+2*y^2

g:=(x,y)->x^2+y^2-1

eq1:=diff(f(x,y), x)=k*diff(g(x,y),x)

eq2:=diff(f(x,y), y)=k*diff(g(x,y),y)

eq3:=g(x,y)=0

ext:=solve( {eq1, eq2, eq3}, {x,y,k} )

subs(ext[1], f(x,y))

subs(ext[2], f(x,y))

subs(ext[3], f(x,y))

subs(ext[4], f(x,y))

---

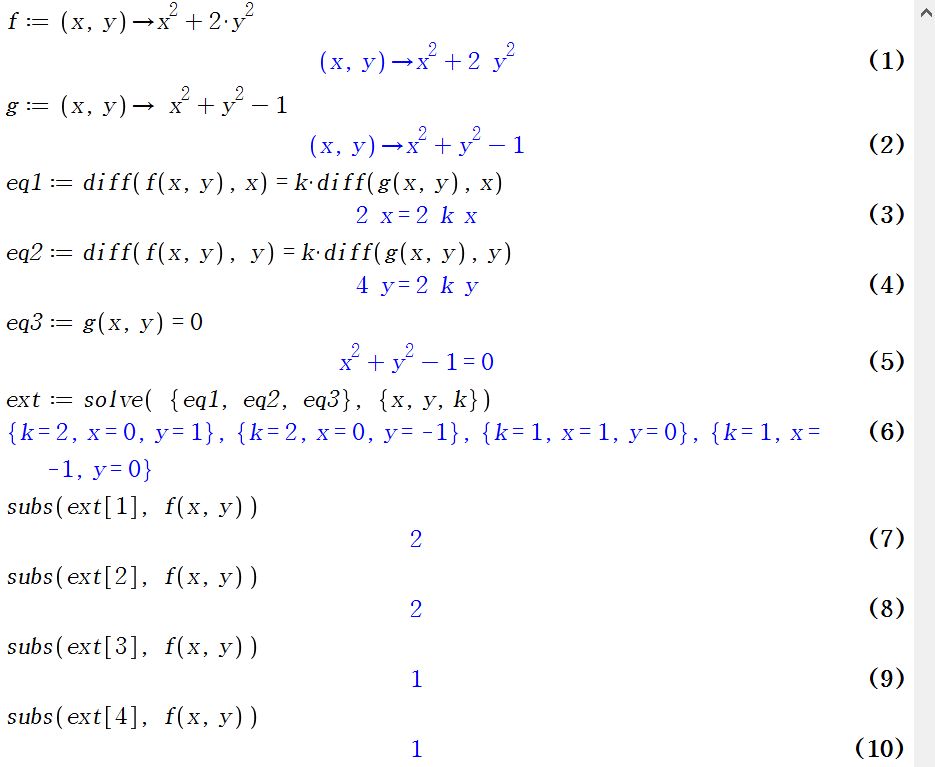
직접해보기

(a). 주어진 함수의 극댓값, 극솟값, 안장점을 구하여라. 만약 3차원 그래프를 그릴 수 있다면 함수의 중요한 부분이 드러날 수 있게 정의역과 방향을 정하여 함수의 그래프를 그려라

"f(x,y)=(exp^x)*cosy"

(b). 라그랑주 승수를 이용하여 주어진 식을 제약조건으로 할 때, 함수의 최대값과 최솟값을 구하여라

"f(x,y,z)=x^2 + y^2 + z^2   ;   x^4 + y^4 + z^4=1"