전산통계학 2차 과제 - 기본연산함수, var 테스트, 행렬

1번) 'x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)' 으로 설정하고, 'range, sum, prod, median, sd' 기능 함수를 직접 만들어보기

 

# range(x) 

x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
range(x)

sm1=function(x){
  c(min(x),max(x))}
sm1(x)

all.equal(range(x),sm1(x))
"It is equal value"

---

 # sum(x) 

x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
sum(x)

sm2=function(x){
  hot=0
  n=length(x)
  for(i in 1:n){
    hot=hot+x[i]
  }
  hot
}
sm2(x)

all.equal(sum(x),sm2(x))
"It is equal value"

---

 # prod(x) 

x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
prod(x)

sm3=function(x){
  cool=1
  n=length(x)
  for(i in 1:n){
    cool=cool*x[i]
  }
  cool
}
sm3(x)

all.equal(prod(x),sm3(x))
"It is equal value"

---

 # median(x)   <ㅡ median 은 주의해야하는 점이, length 가 짝수|홀수 일 때, 계산되는 원리가 다름을 인지하셔야 해요

x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
median(x)
z<-sort(x)
z

sm4=function(x) {
  n=length(x)
  for (i in 1:n) {
    if((1+n)%%2==0) {oh=z[(1+n)/2]}
    else {(oh=z[n/2]+z[(n/2)+1])/2}
  }
  oh
}
sm4(x)

all.equal(median(x),sm4(x))
"It is equal value"

---

# sd(x) 

x<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
sd(x)

sm5=function(x){
  n=length(x) ; m=mean(x)
  lol=0
  for(i in 1:n ) {
    lol=lol+(x[i]-m)^2
  }
  sqrt(lol/(n-1))
}
sm5(x)

all.equal(sd(x),sm5(x))
"It is equal value"

---

2번) 'x1<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
, x2<-c(2.39,2.56,2.36,2.62,2.51,2.29,2.58,2.41,2.86,2.49,2.33,1.94,2.14)' 으로 설정하고,

var.test : statistic, p-value, conf.int 을 한 번에 출력하는 함수 만들기

<단, 출력값은 "f* = x.xxx , p-value = xx , confidence interval = (lower bound, upper bound) 값" 으로 출력하기>

 

x1<-c(1.79,1.87,1.62,1.96,1.75,1.74,2.06,1.69,1.67,1.94,1.33,1.70,1.65)
x2<-c(2.39,2.56,2.36,2.62,2.51,2.29,2.58,2.41,2.86,2.49,2.33,1.94,2.14)

var.test(x1,x2,ratio=1,alternative=c("two.sided"))$'statistic'
var.test(x1,x2,ratio=1,alternative=c("two.sided"))$'p.value'
var.test(x1,x2,ratio=1,alternative=c("two.sided"))$'conf.int'

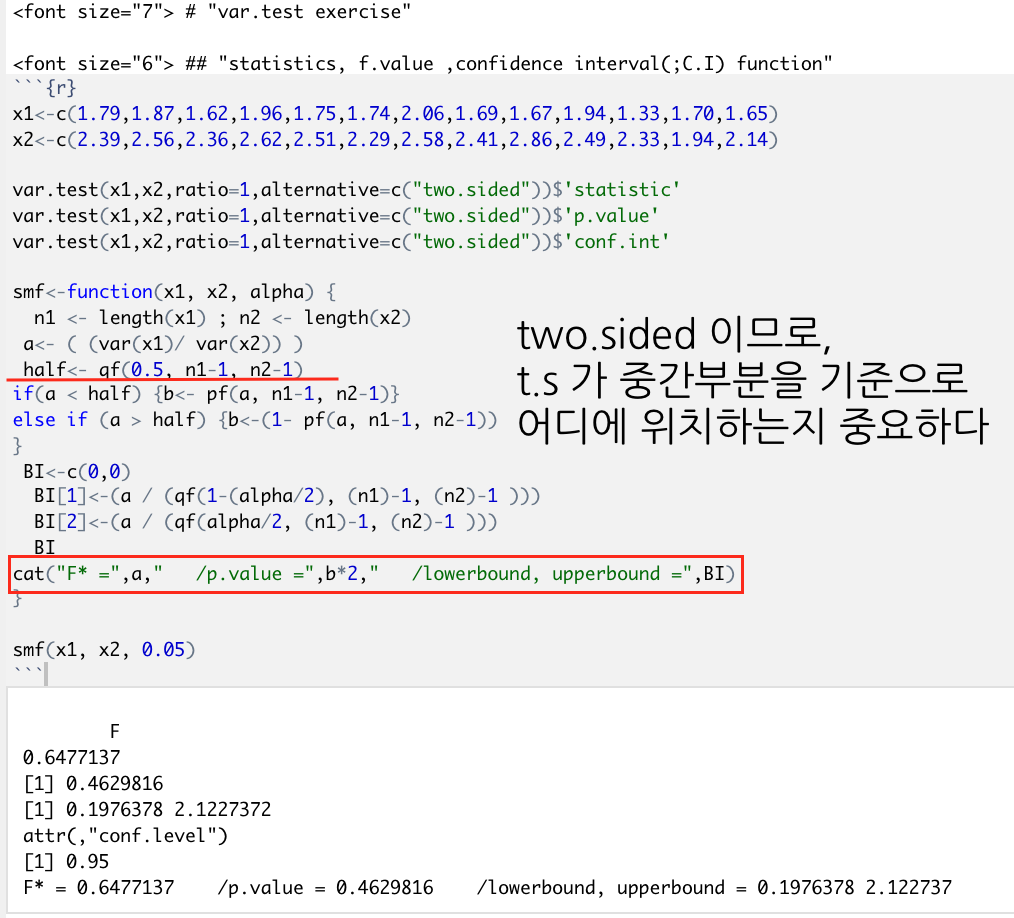
smf<-function(x1, x2, alpha) {
  n1 <- length(x1) ; n2 <- length(x2)
 a<- ( (var(x1)/ var(x2)) )
 half<- qf(0.5, n1-1, n2-1)
if(a < half) {b<- pf(a, n1-1, n2-1)}
else if (a > half) {b<-(1- pf(a, n1-1, n2-1))
}
 BI<-c(0,0)
  BI[1]<-(a / (qf(1-(alpha/2), (n1)-1, (n2)-1 )))
  BI[2]<-(a / (qf(alpha/2, (n1)-1, (n2)-1 )))
  BI
cat("F* =",a,"   /p.value =",b*2,"   /lowerbound, upperbound =",BI)
}

smf(x1, x2, 0.05)

---

3번) (1). i번째에서 i+5번째까지 원소들을 더한 후, 길이가 95인 벡터를 만든다 ㅡ> 이 중, 3의 배수 개수를 출력

(2). i번째에서 i+4번째까지 원소들을 더한 후, i+5번째는 곱한 후, 길이가 95인 벡터를 만든다 ㅡ> 이 중, 4의 배수 개수 출력

 

# 3배수 개수   (95개 나오면 정답)

x<-(1:100)
sm3mu.<-function(x) {
  for (i in 1:95) {
    x[i]<-(6*i+15)
  }
  y<-x[1:95]
  for (j in 1:95) {
    if (y[j]%%3==0) {
      y[j]<-0
    }
  }
  length(y[y==0]) 
}
sm3mu.(x)

---

# 4배수 개수   (48개 나오면 정답)

x<-(1:100)
sm4mu.<-function(x) {
  for (i in 1:95) {
    x[i]<-(5*i^2 + 35*i + 50)
  }
  y<-x[1:95]
  for (j in 1:95) {
    if (y[j]%%4==0) {
      y[j]<-0
    }
  }
  length(y[y==0]) 
}
sm4mu.(x)

---

<과제 총평>

1번 : median 의 원리만 잘 생각하면 끝인 것 같아요

 

2번 : 사실 var.test 보다는, cat으로 결과값 정리할 수 있는가? 를 판단하는 문제로 보여요

 

3번 : 필자의 개인적인 추천으로는 제가 만든 위의 함수보다는, which 를 써서 만들어 보시는 것을 추천해요