전산통계학 5차 과제 - 행렬 곱, apply(2차원), array, apply(3차원)

1번) 1~100까지 두개의 sample matrix A(= 10x15) 와 B(=15x20) 을 생성하고, A%*%B 와 동일한 값을 가지게끔 연산 작용을 하는 함수를 만드세요 (단, 행렬 원소를 곱하는 과정에서 명령어가 아닌 연산원리를 그대로 함수에 적용할 수 있도록... , 그리고 dimension 이 바뀌어도 돌아가게끔 일반화 시키세요!)

 

X<-matrix ; Y<-matrix

matmultip<-function (X,Y) {
  l<-nrow(X) ; m<-ncol(X) ; k<-ncol(Y)
  C<-matrix(nrow=l,ncol=k)
  if (nrow(Y)==m){
  for (i in 1:l) {
    for (j in 1:k) {
      C[i,j] <-sum(X[i,1:m]*Y[1:m,j])
    }
  }
  C
  }
  else {cat("The two matrices cannot be multiplied.")}
}

A<-matrix(sample(1:100, 150, T),10,15)
B<-matrix(sample(1:100, 150, T),15,20)
A%*%B 
matmultip(A,B)

all.equal(A%*%B,matmultip(A,B))


"If two matrix is can't multiply, what is this functions answer?"
E<-matrix((1:10),5,2)
G<-matrix((1:12),4,3)
matmultip(E,G)

---

2번) matrix 에서 apply 와 똑같은 값이 나오게끔 하는 함수를 만드세요

(단, sum, mean 또한 변수로 넣어야 하고, sum, mean 명령어는 사용하면 안됩니다

그리고, 1,2 는 apply 처럼 행,열로 작용하게끔 하는 변수로...)

#Data

x <- matrix(1:12, nrow=3, ncol=4)

sm<-function(x,num,q) {
  mo <- rep(0,dim(x)[num])
  so <- rep(0,dim(x)[num])
  
  for (i in 1: nrow(x)) {
    for (j in 1: ncol(x)) {
      if (num==1) {
        if (q=="sum") {A <- x[i,]
        mo[i] <- mo[i]+A[j]}
        if (q=="mean") {A <- x[i,]
        so[i] <- so[i]+A[j]
        mo[i] <- so[i]/ncol(x)}
      }
      if (num==2) {
        if (q=="sum") {A <- x[,j]
        mo[j] <- mo[j]+A[i]}
        if (q=="mean") {A <- x[,j]
        so[j] <- so[j]+A[i]
        mo[j] <- so[j]/nrow(x)}
    }
  }
  }
  mo
}

sm(x,1,"sum") ; apply(x,1,sum)
sm(x,1,"mean"); apply(x,1,mean)
sm(x,2,"sum") ; apply(x,2,sum)
sm(x,2,"mean"); apply(x,2,mean)

---

3번) array 에 관한 문제인데, 행렬의 데이터는 c(1:12) 로 고정하고, 2개의 차원이 생기게끔 할 것입니다.

그런데, 원래의 array 데이터 형성 원리와 다르게, 마치 byrow=T 를 적용한 것처럼 데이터가 채워지는 꼴로 array 짜세요# Original matrix w 
w <- array(1:12, dim=c(2,3,2))
w


byrow <-  function (x) {
  M <- list()
  d <- dim(x)
  i <- d[1] ; j <- d[2] ; num <- d[3]
  n <- length(x)
  
  for (z in 1:num) {
    M[z] <- list(matrix (c( (1+i*j*(z-1) ):(i*j*z) ), i,j, byrow = T))
  }
  M
}
byrow(w)

# Other example (different dimension)
p <- array(1:24, dim=c(3,2,4))
p ; byrow(p)

---

4번) 위에서 다루었던 '2번' 문제처럼, 이번에는 array 에서 apply 의 sum 과 동일하게 연산작용을 하는 함수를 만드세요 

(2번 문제와 달리 1,2 에서 3(=차원) 까지 생각해야 합니다)

# Data

x <- array(1:12, dim=c(2,3,2))

sm <- function(x,num) {
  su=rep(0,dim(x)[num])
  A= list() ; B= list() ; C= list()
         
         for(i in 1:dim(x)[1]) {
           for(j in 1:dim(x)[2]) {
             for(k in 1:dim(x)[3]){
               if(num==1) {A[[i]] <- x[i,,]
               su[i] <- su[i]+ A[[i]][j,k] }
               
               if(num==2) {B[[j]] <- x[,j,]
               su[j] <- su[j]+B[[j]][i,k] }
               
               if(num==3) {C[[k]] <- x[,,k]
               su[k] <- su[k]+C[[k]][i,j] }
             }
           }
         }
su
  }
sm(x,1) ;apply(x, 1, sum)
sm(x,2) ;apply(x, 2, sum)
sm(x,3) ;apply(x, 3, sum)

---

<과제 총평>

1번 : 선형대수학을 잘 공부했다면, 쉬웠을 거에요

(만약, 감이 오지 않는다면 A=3x2, B=2x4 행렬로 원소를 적당히 주고, 행렬을 곱할 때, 어떤 원소끼리 곱해지는지 손으로 써가면 이해할 수 있을겁니다)

 

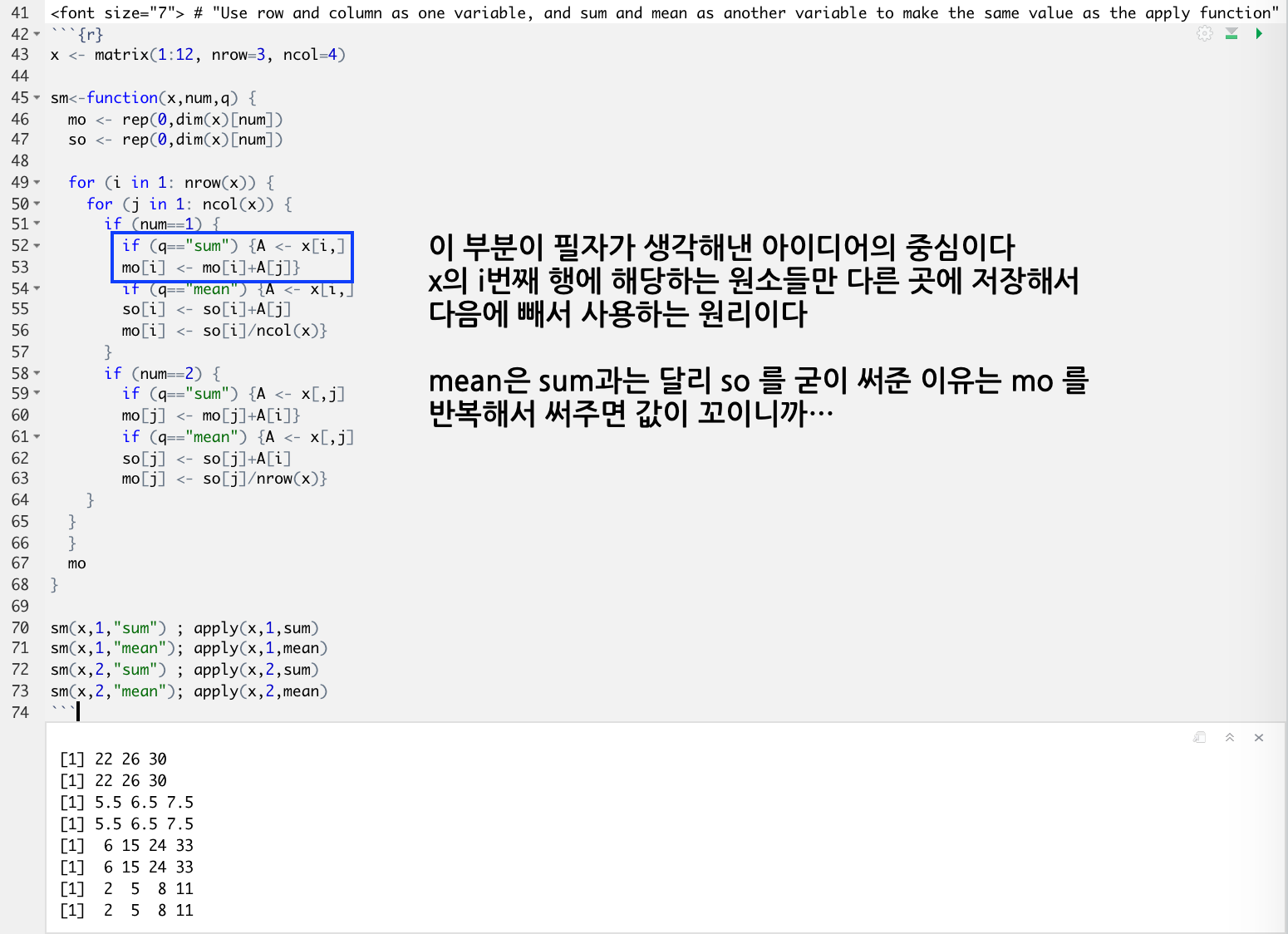
2번 : 아마, 함수가 제한이 걸려있어서 아이디어를 생각해내는데, 조금 애를 먹었던 문제로 기억합니다

 

3번 : 사실 필자처럼 array 된 w 자체를 이용해서, 원소 배열 규칙으로 함수를 만들면 감점이 됩니다...

(실제로, 당시에 array 자체 함수를 변수로 넣어서 과제를 한 인원들은 감점을 받았습니다...)

그러므로, array 된 w 를 변수로 사용하지 않고, 다른 함수를 만들어가며 공부하는 것을 추천합니다!

 

4번 : 아마 위에서의 설명이 필자가 말재주가 없어서 못 이해하시는 분이 많을 것 같아요...

추가로 설명하자면, 아래의 사진을 보면, 형성된 행렬의 총 행과 열의 개수에 특징을 생각하시면, 쉬울 겁니다