전산통계학 12주차 강의 - factorial experiments, Interaction, signtest

SignTest

# DATA (283p.)

data <- c(35,65,48,40,70,50,58,36,47,41,49,39,34,33,31)

 

library(DescTools)

SignTest(DATA, mu = 55, alternative = "two.sided")

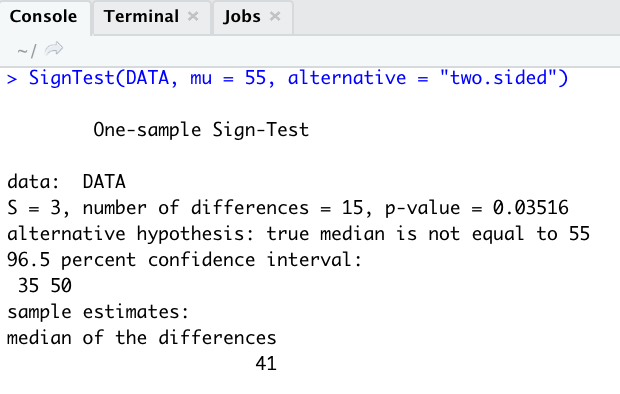
위의 사진은 'desctools' 패키지에 속해있는 'SignTest' 명령어를 이용해서 two tails & M0=55 (=mu) 일 경우를 검정한 결과

---

<문제>

그렇다면, 우리들은 'SignTest' 를 함수로, 즉 프로그래밍 해서 당연히 만들어 볼 수 있지 않을까요???

sm <- function(x, muzero, side) {
  equal=0 ; low=0 ; high=0
  
  for (i in 1: length(x)) {
    if(x[i]==muzero) {equal=equal+1} 
    
    else if (x[i]<muzero) {low=low+1} 
    
    else {high= high+1} 
  }
  if (low<high) {low=low+equal}
  
  qstar  <-  low
  
  if (side=="two.sided") {
    pvalue <- min( 1- pbinom(qstar-1, length(x), 0.5), pbinom(qstar,length(x), 0.5))*2
  }
  
  if (side=="less") {
    pvalue <- 1-pbinom(qstar - 1, length(x), 0.5)
  }
  
  else if (side=="greater") {
    pvalue <- pbinom(qstar , length(x), 0.5)
  }
  cat("\n",side ,"of Sign-Test","\np-value =",pvalue,
      "\nCompare with SignTest ft. in R =", SignTest(DATA, alternative = side, mu=muzero)$p.value)
}

---

<첨언>

하지만, 수리통계학을 열심히 들은 사람은 필자가 만든 함수에 큰 오류가 있음을 알 수 있을 것에요....

만약, 찾기 힘들다면 다음과 같은 데이터 (handeling in zeros) 를 새로 만들어서 하나는 SignTest로,

또 다른 하나는 필자가 만든 함수에 넣어서 값을 구해보면 두 개의 이상한 점을 볼 수 있을 것 입니다

ADDDATA  <- c(35,65,48,40,70,50,58,36,47,41,49,39,34,33,31 ,55,55,55,55,55)

(여기서 못 찾으시더라도, 나중에 과제에서 자세히 다루어 볼터이니, 걱정은 안하셔도 됩니다)

---

Factorial Experiments - interaction test

# data (575p.) <- matrix(c(40,36,43,36,34,39,
          39,36,33,32,26,25,
          32,34,29,26,23,24,
          33,27,25,20,22,18),6)

 

A <- gl(4,6)
B <- factor (rep (1:2,each=3, len=24))
C <- gl(8,3)

fac <- function (data, A, B, C, alpha) {
  n <- length(data)/ length( levels(C) ) ; a <- length( levels(A) ) ; b <- length( levels(B) )
  
  dftrt <-  a*b-1 ; dfa <- a-1 ; dfb <- b-1 ; dfab <- (a-1)*(b-1) ; dferror <- a*b*(n-1)
  
  t... <- sum(data) ; tij. <- matrix(tapply(data, C ,sum),2) ; ti.. <- tapply(data, A, sum) ; t.j. <- tapply(data, B, sum)
  
  sstrt <- sum(tij.^2/n) - t...^2/(a*b*n) ; ssa <- sum(ti..^2/(b*n)) - t...^2/(a*b*n)
  ssb <- sum(t.j.^2/(a*n)) - t...^2/(a*b*n) ; ssab <- sstrt-ssa-ssb ; sstot <- sum(data^2) -t...^2/(a*b*n) 
  sserror <- sstot-sstrt
  
  mstrt <- sstrt/dftrt ; msa <- ssa/dfa ; msb <- ssb/dfb ; msab <- ssab/dfab ; mserror <- sserror/dferror
  
  f1 <- mstrt/mserror
  f2 <- msa/mserror
  f3 <- msb/mserror
  f4 <- msab/mserror
  
  inter.pvalue <- pf (f4, dfab, a*b*(length(levels(C))-1), lower.tail = F)
  
  cat("F* of interaction=", f4, "\np-value=", inter.pvalue)
}

fac(data,A,B,C)

---

<문제>

위의 사진에서 언급했던 것 처럼... interaction test 에 따라서 그 후의 두가지 케이스로 향하게끔 프로그래밍 하고, 그에 따른 결과들을 보기 쉽게 테이블로 정리해서 보여줄 수 있을까요?