전산통계학 13주차 강의 - agricolae, AOV, Post Hoc (Bonferroni, Scheffe, Duncan, Tukey)
코딩 공부/R-전산 통계학 2020. 1. 20. 23:16AOV (Fit an Analysis of Variance Model)
data <- c(40,36,43,36,34,29,
39,36,33,32,26,25,
32,34,29,26,23,24,
33,27,25,20,22,18)
A <- gl(4,6)
B <- factor (rep (1:2,each=3, len=24))
C <- gl(8,3)
aov(data~A*B) ; "data 가 매트릭스여서 c; 벡터형태로 주어야합니다!"
summary(aov(data~A*B))
summary(aov(data~A+B+A*B)) ; "Same"

<첨언>
Case of 3 factors?
data <- c(42,38, 28,22, 34,10,
34,34, 28,08, 19,08,
33,41, 11,03, 17,00,
47,38, 52,33, 22,16,
59,41, 33,15, 03,10,
43,32, 29,24, 17,01,
55,48, 54,27, 17,22,
66,26, 36,41, 40,06,
69,63, 53,38, 40,38,
64,58, 63,41, 33,29,
60,51, 55,40, 34,24,
94,67, 40,64, 40,20)
length(data)
A <- factor (rep(1:3, each=2, 12))
B <- gl(4,18)
C <- factor (rep(1:2,each=1, 36))
summary(aov(data~A*B*C))
<문제>
3 factors 에서 "α*γ 그리고 α*β*γ" 항목을 표에 안나오도록 설계할 수 있을까요?
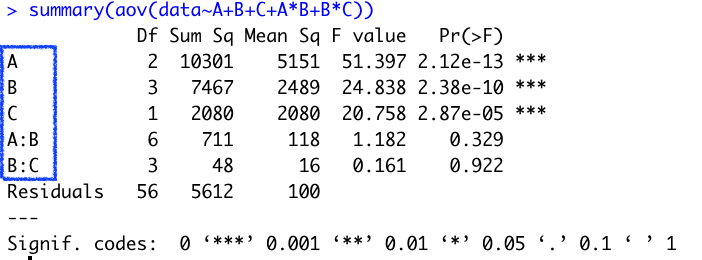
data <- c(42,38, 28,22, 34,10,
34,34, 28,08, 19,08,
33,41, 11,03, 17,00,
47,38, 52,33, 22,16,
59,41, 33,15, 03,10,
43,32, 29,24, 17,01,
55,48, 54,27, 17,22,
66,26, 36,41, 40,06,
69,63, 53,38, 40,38,
64,58, 63,41, 33,29,
60,51, 55,40, 34,24,
94,67, 40,64, 40,20)
A <- factor (rep(1:3, each=2, 12))
B <- gl(4,18)
C <- factor (rep(1:2,each=1, 36))
summary(aov(data~A+B+C+A*B+B*C))
<첨언>
행렬 원소를 x[ a,b ] 와 같은 형식으로 값을 뽑아낼 수 있었는데, aov 에서도 값을 뽑아내는 것이 가능할까?

우리는 ANOVA 에서 가설 (null hypothesis , alternative hypothesis) 을 세우고, 테스팅을 진행하여 reject H0 에 수긍했다는 결론을 얻고나서, 본 수업 (확률론이나 수리통계학) 에서는 Bon-ferroni 나 Scheffe 방법을 이용해서 각 그룹에 따라서 어떤식으로 다른지 알아볼 수 있었다. 지금 하는 전산통계학에서는 여러개의 그룹을 프로그래밍만 잘 짜본다면 한 번의 함수만에 모든 그룹을 각각 비교할 수 있다
library(agricolae)
data<-c(1.51, 1.92, 1.08, 2.04, 2.14, 1.76, 1.17
,1.69, 0.64, 0.90, 1.41, 1.01, 0.84, 1.28, 1.59
,1.56, 1.22, 1.32, 1.39, 1.33, 1.54, 1.04, 2.25, 1.49
,1.30, 0.75, 1.26, 0.69, 0.62, 0.90, 1.20, 0.32
,0.73, 0.80, 0.90, 1.24, 0.82, 0.72, 0.57, 1.18, 0.54, 1.30)
a <- factor (rep(1:5, c(7,8,9,8,10)))
# 1. DUNCAN
model2 <- aov(data~a)
result <- duncan.test(model2, "a", main ="real", alpha = 0.01)
plot(result, variation = "IQR")

# 2. SCHEFFE
model3 <- aov(data~a)
answer <- scheffe.test(model3, "a", alpha = 0.01)
plot(answer, variation = "IQR")

# 1. DUNCAN 과 다른 모양의 plot 이 나올 수도 있음을 알 수 있다.
# 3. TUKEY (HSD.test)
model4 <- (aov(data~a))
dap <- HSD.test(model4,"a",alpha=0.01)
plot(dap, variation = "IQR")

# 4. Bonferroni (LSD.test)
model5 <- (aov(data~a))
dap <- LSD.test(model5,"a",alpha=0.05,p.adj = "bonferroni",group = TRUE)
plot(dap, variation="IQR")

마지막으로 말을 덧붙이자면... 교재와 그룹(13245 사이에 밑줄이 쳐져있는 부분이 제가 한 것과 다를 수 있습니다, 그 이유로는 필자는 유의수준을 모두 0.95로 고정한 점도 있고, 문자가 포함되있냐 안되있냐에 따른 기준으로 같은 그룹이 될 수 있는 여부에 따라서 밑줄을 친 것이기 때문에, 한 번 고려해보면서 스스로 생각해보시는 거를 추천합니다
<문제>
data <- c(9.1, 13.4, 15.6, 11.0, 12.7,
17.1, 20.3, 24.6, 18.2, 19.8,
20.8, 28.3, 23.7, 21.4, 25.1,
11.8, 16.0, 16.2, 14.1, 15.8)
A <- gl(4,5)
B <- factor(rep(1:5,4))
다음과 같은 데이터 형태를 가지고 있는 R.C.B.D 를 trt factor 에 따라서 그룹마다 어떻게 차이나는지 DUNCAN 기법 분석해보세요
model <- aov(data~A+B)
summary(model)
out<- duncan.test(model, "A",alpha = 0.01)
plot(out, "IQR")
 TAG
TAG






