전산통계학 7차 과제 - 구 만들기, plot, legend
코딩 공부/R-전산 통계학 2020. 2. 5. 13:511번) 'graphics1 handouts.pdf' 파일을 진행하다 보면, 첨부해둔 사진처럼 예시를 보이기 위한 명령문들이 보일텐데, 그 명령어를
직접 입력하되 입력값 또는 출력색 등을 스스로 변경해서 진행하세요 (예시 개수 : 24개)
따라서, 노가다 과제이기 때문에, 전체 명령어를 이 글에 기재하지는 않도록 하겠음

혹여나, 이해가 잘 되지 않는다면 다음 사진을 참고해서 진행해보도록 하세요
2번) 'persp' 함수를 사용해서 구(sphere) 를 생성함과 동시에 구의 중심점을 점으로 표시 및 텍스트를 출력하고,
구의 중심점을 지나는 화살표를 만드세요
# Data
x <- y <- seq(-1,1,len=64)
z1 <- z <- outer(x,y,FUN=function(x,y) x^2+y^2)
# Setting z
for(i in 1:length(x)){
for(j in 1:length(y)){
if(z[i,j]>0.98 & z[i,j]<=1.02) z[i,j]=0
else if(z[i,j]>1.02) z[i,j]=NA
else z[i,j]= sqrt(1-z[i,j])
}
}
for(i in 1:length(x)){
for(j in 1:length(y)){
if(z1[i,j]>0.98 & z1[i,j]<=1.02) z1[i,j]=0
else if(z1[i,j]>1.02) z1[i,j]=NA
else z1[i,j]= -sqrt(1-z1[i,j])
}
}
# Persp
persp(x,y,z1,
axes=T,
box=T,
zlim=c(-1,1),
col="white",main="Sphere",
border="aquamarine",
theta=15)-> Lee1
par(new=T)
persp(x,y,z,
axes=F,
box=F,
zlim=c(-1,1),
col="white",main="Sphere",
border="aquamarine",
theta=15) -> Lee
points(trans3d(0,0,0,Lee),cex=1,pch=19 ,col="black", bg="gold")
text(trans3d(0,0,0,Lee),pos=1,labels="(0,0,0)",cex=1,col="black")
text(trans3d(0.4,-0.5,0,Lee),pos=1,labels="Lee Seung Mock",cex=1,col="black")
# Line
lines(trans3d(c(-.75,-0.5),c(-.75,-0.5),c(-.75,-0.5),Lee),lwd=3, col="Red")
lines(trans3d(c(-0.5,0.7),c(-0.5,0.7),c(-0.5,0.7),Lee),lty=3 ,lwd=3, col="Red")
lines(trans3d(c(0.7,1),c(0.7,1),c(0.7,1),Lee),lwd=3, col="Red")
lines(trans3d(c(.8,1),c(.7,1),c(.5,1),Lee),lwd=3, col="Red")
lines(trans3d(c(.5,1),c(.7,1),c(.8,1),Lee),lwd=3, col="Red")
2번 문제 추가 해설 - 1

위의 명령어를 살펴보면 z (혹은 z1) outer들을 설정할 때, z[i,j]==1 이 아닌, (0.98, 1.02) 의 구간에 대해서 설정을 해주었는데, 그 이유는 다음 사진을 보면 알 수 있습니다
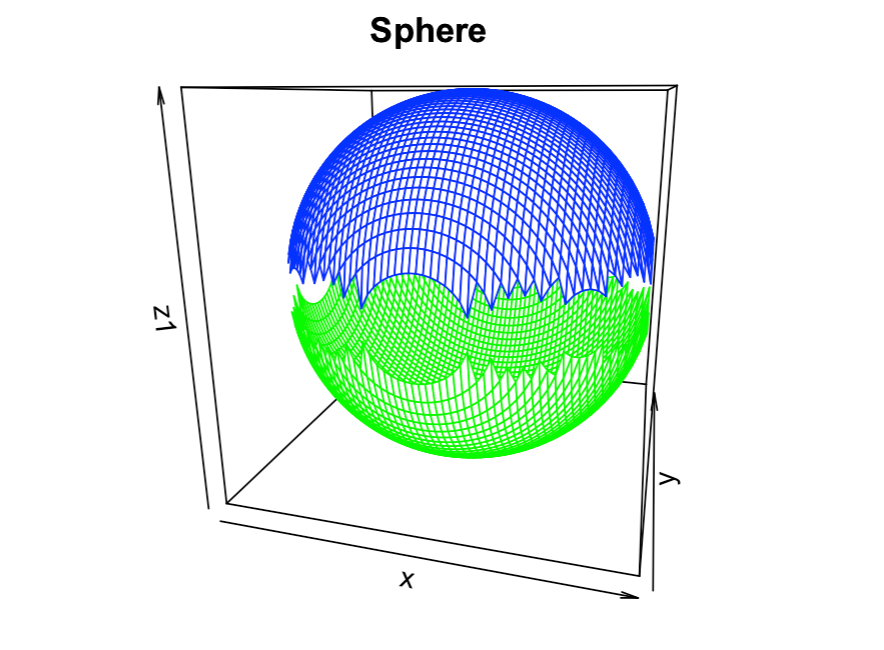
두 개의 persp 가 깔끔하게 합쳐지지 않고, '이빨' 과 같은 틈이 벌어짐을 볼 수 있는데, 이는 수학과의 전공 중, 복소해석학 + 고급해석학
을 배우셨다면 충분히 이해하실 수 있어요
(그래도 이해가 안되신다면, x와 y를 (-1,1) 구간 수열로 잡고, z='x^2 + y^2' 의 행렬로 출력하게끔 만드시면 이상한 점을 보실 수 있습니다)
2번 문제 추가 해설 - 2
사실 이 구를 만들어보라는 교수님의 과제를 받자마자 여러분들이 하실 생각이 다음과 같이 2가지로 크게 나뉘는데, 각각의 까다로운 점이 존재할 겁니다.
1번째 : 나는 z가 x,y 두 변수에 대한 outer 인데, 이에 대한 x,y의 식이 "x^2 + y^2" 이기 때문에, 생성되어지는 z에 '음수'가 없다?
2번째 : 나는 두 개의 persp 를 생성해서 두개를 합치려고 하는데, 도대체 어떻게 해야 합쳐지는거지?
이에 대한 저의 대답은... 1번째 방법에서 저 관계식으로 +,- 를 동시에 가지는 z를 생성시키는 방법은 제가 알기로는 없는 것으로 압니다
그러나 2번째 방법은 충분히 잘 생각하셨으나, 'par' 함수를 모르기 때문에 어쩔 수 없이 막히게 됩니다
따라서 다음 사진을 참고해보면 위의 해설된 명령어의 구조를 더 이해하기 쉬울 것 같습니다

3번) 함수에 변수를 1~3 을 넣음으로써,
함수(1) = 한자 金
함수(2) = 한자 王
함수(3) = 위의 두 한자 모두 출력되게끔 plot을 이용한 함수를 만들어보세요
(단, 모든 선분을 최대한 다른 타입의 선분, 다른 굵기로 생성, 그리고 한자 王은 한자 金의 1/4 사이즈로 생성하게끔 만드세요)
f <- function(c) {
plot.new()
if(c==1) {plot.window(xlim=c(0,10),
ylim=c(0,10), asp=0)
lines(c(0.1,5),c(6,10) ,col = "red", type = "o", lty=2, lwd=8, pch=1)
lines(c(9.9,5),c(6,10) ,col = "orange", type = "o", lty=3, lwd=1, pch=1)
lines(c(5,5),c(0,10) ,col = "gold", type = "o", lty=4, lwd=7, pch=1)
lines(c(1,9),c(6,6) ,col = "forest green", type = "o", lwd=2, pch=1)
lines(c(0.1,9.9),c(4,4) ,col = "dark blue", type = "o", lty=2, lwd=6, pch=1)
lines(c(0.1,9.9),c(0,0) ,col = "cyan", type = "o", lty=3, lwd=3, pch=1)
lines(c(3,5),c(2,0) ,col = "purple", type = "o", lty=4, lwd=5, pch=1)
lines(c(7,5),c(2,0) ,col = "grey", type = "o", lwd=4, pch=1)
axis(1) ; axis(2 , las=1)
box()
title (main= "金")
}
if(c==2) {plot.window(xlim=c(0,10),
ylim=c(0,10), asp=0)
lines(c(2.5,7.5), c(5,5), col="orchid", type="l", lty=2,lwd=8 , pch=1)
lines(c(2.5,7.5), c(2.5,2.5), col="plum", type="l", lty=3, lwd=6 , pch=1)
lines(c(2.5,7.5), c(0,0), col="deep pink", type="l", lty=4, lwd=4 , pch=1)
lines(c(5,5), c(0,5), col="light slate blue", type="l", lwd=2 , pch=1)
axis(1) ; axis(2, las=1)
box()
title (main= "王")
}
if(c==3) {plot.window(xlim=c(-5,10),
ylim=c(0,10), asp=0)
lines(c(0.1,5),c(6,10) ,col = "red", type = "o", lty=2, lwd=8, pch=1)
lines(c(9.9,5),c(6,10) ,col = "orange", type = "o", lty=3, lwd=1, pch=1)
lines(c(5,5),c(0,10) ,col = "gold", type = "o", lty=4, lwd=7, pch=1)
lines(c(1,9),c(6,6) ,col = "forest green", type = "o", lwd=2, pch=1)
lines(c(0.1,9.9),c(4,4) ,col = "dark blue", type = "o", lty=2, lwd=6, pch=1)
lines(c(0.1,9.9),c(0,0) ,col = "cyan", type = "o", lty=3, lwd=3, pch=1)
lines(c(3,5),c(2,0) ,col = "purple", type = "o", lty=4, lwd=5, pch=1)
lines(c(7,5),c(2,0) ,col = "grey", type = "o", lwd=4, pch=1)
lines(c(-5,0), c(5,5), col="orchid", type="l", lty=2, lwd=8 , pch=1)
lines(c(-5,0), c(2.5,2.5), col="plum", type="l", lty=3, lwd=6 , pch=1)
lines(c(-5,0), c(0,0), col="deep pink", type="l", lty=4, lwd=4 , pch=1)
lines(c(-2.5,-2.5), c(0,5), col="light slate blue", type="l", lwd=4 , pch=1)
axis(1) ; axis(2, las=1)
box()
title (main= "both 金 and 王")
}
}
f(1) ; f(2) ; f(3)


4번) 아래에 첨부한 사진과 같은 plot 을 만들어 보세요 (원래의 데이터는 수업시간에 진행하면서 받게 될 것 입니다)

# Data
set.seed(789)
x1 <- rnorm(10); x2 <- rnorm(10, mean=2)
y1 <- rnorm(10); y2 <- rnorm(10, mean=2)
sx1<- sort(x1) ; sx2 <- sort(x2)
sy1<- sort(y1) ; sy2 <- sort(y2)
plot(range(x1,x2), range(y1,y2), main="Home work 7-4", type="n", xlab="X", ylab="Y")
lines(sx1, sy1, col="Red", type="l", pch=1) # Group 1
points(sx1, sy1, col="white", pch=19)
points(sx1, sy1, col="black", pch=1)
lines(sx2, sy2, col="blue", type="o", pch=0) # Group 2
a <- max(x1) ; b <- max(y1)
c <- min(x2) ; d <- min(y2)
points(c(a,c), c(b,d), col="white", pch=c(19,15), cex=1.2)
lines(c(a,c),c(b,d), col="red", type="l")
lines(sx1, sy1, col="Red", type="l") # Group 1
lines(sx2, sy2, col="blue", type="l") # Group 2
points(sx1[-which(sx1==a)], sy1[-which(sy1==b)], col="white", pch=19)
points(sx1[-which(sx1==a)], sy1[-which(sy1==b)], col="black", pch=1)
legend(-2, 2.5, c("Group 1", "Group 2"), pch=c(19,0), col=c("red", "blue"), horiz=F, bty="n", lty=1)
<과제 총평>
1번 : 단순히 입력 값을 변경하며 시간을 오래 들이는 메가스터디 3000제 같은 문제이므로, 오래걸리는 점을 제외하면 쉬움
2번 : 전산통계학을 하며 만나게 되는 '지옥 문제' 중에 첫 번째로 나오게 되는 문제에요, 구글에 검색을 해도 극소수의 자료밖에 볼 수 없고, 'par(new+T)' 를 따로 배우지를 않았기 때문에, 생각해내기 정말로 어려운 문제로 생각이 됩니다
3번 : plot 과 함수를 합친 단순한 문제
4번 : 문제에서 까다로웠던 점은 "왼쪽 선분의 동그라미 점 내부에 붉은 선분을 어떻게 없앨까?" 라는 아이디어를 캣치하는게 까다로웠을 것
 TAG
TAG






