전산통계학 8차 과제 - 삼중적분, 삼중미분, 감마함수, 싸인테스트

 

 

http://tutorial.math.lamar.edu/Classes/CalcIII/TripleIntegrals.aspx

Calculus III - Triple Integrals

1번) 위의 사진은 기재되어있는 링크에 있는 삼중적분 문제이다, 이 삼중적분을 패키지 'pracma' 내의 명령어인 'integral3' 를 사용해서 삼중 적분을 하고, R의 값과 링크에 기재되어 있는 값을 비교해보세요.

이 다음으로 패키지 'TeachingDemos' 를 사용해서 위의 기재되어있는 그림과 동일한 persp 를 형성하세요 (축의 변경은 상관x)

 

# 1-1. tri integral

library(pracma)

sm <- function(x, y, z) sqrt(3*x^2 + 3*z^2)

# bounded by (y=2*x^2 + 2*z^2 & y<=8)
xmin <- -2
xmax <- 2
ymin <- function(x) 2*x^2
ymax <- 8
zmin <- function(x,y) -sqrt ( (y-2*x^2)/2 )
zmax <- function(x,y) sqrt ( (y-2*x^2)/2 )

integral3 (sm, xmin,xmax, ymin,ymax, zmin,zmax)

# linear value
(256*sqrt(3)*pi)/15

 

 

 

# 1-2. Persp
library(TeachingDemos)

z<- x <- seq(-2, 2 ,len=200)
y <- outer(x,z, FUN = function(x,z) 2*(x^2+z^2)) 

for(i in 1: ncol(y)) {
  for (j in 1: nrow(y)) {
    if (y[i,j]>7.95 & y[i,j]<8.05) {y[i,j] <- 8}
    else if (y[i,j]>8.05) {y[i,j] <- NA}
  }
}
persp(x,z,y,
      axes = T, box = T
      ,xlim = c(-3,3), zlim = c(0,9), ylim = c(-3,3)
      , shade=0.8
      , col="red", border = "forest green", theta = 30,
      main = "exercise of triple integrate") -> exe

par(new=T)

z<- x <- seq(-2, 2 ,len=200)
y1 <- outer(x,z, FUN = function(x,z) 2*(x^2+z^2)) 

for(i in 1: ncol(y1)) {
  for (j in 1: nrow(y1)) {
    if (y1[i,j]<8.05) {y1[i,j] <- 8}
    else {y1[i,j] <- NA}
  }
}
persp(x,z,y1,
      axes = F, box = F
      ,xlim = c(-3,3), zlim = c(0,9), ylim = c(-3,3)
      , shade=0.8
      , col="blue", border = "cyan", theta = 30,
      main = "exercise of triple integrate")

points(trans3d(0,0,0,exe),cex=1,pch=19 ,col="black", bg="gold")
text(trans3d(0,0,0,exe),pos=1,labels="(0,0,0)",cex=1,col="black")
points(trans3d(0,0,8,exe),cex=1,pch=19 ,col="black", bg="gold")
text(trans3d(0,0,8,exe),pos=1,labels="(0,8,0)",cex=1,col="black")

 

 

---

2번) 확률론 시간에 언급되는 'Gamma Density' 에 대해서 실제 함수를 짜보고, alpha=3.5, beta=3.0 에 대해서 적분 값을 구하세요,

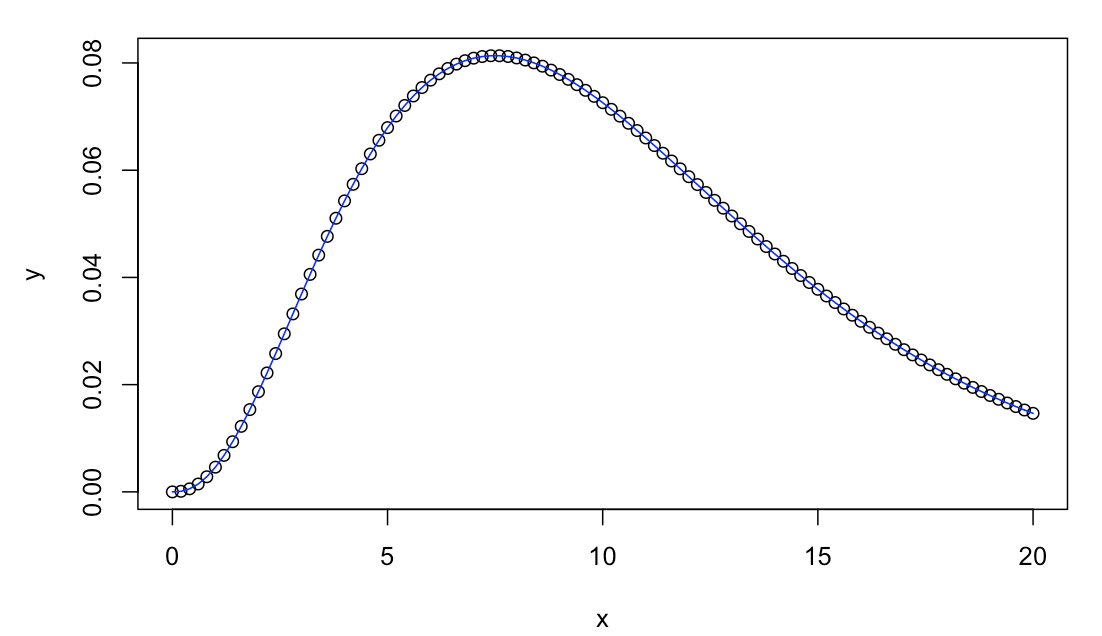
그 값과 R내에 있는 'dgamma' 를 이용한 적분 값을 비교하고, 그래프로 차이가 있는지 가능하면 보여주세요

 

# 2-1. plot gamma distribution (compare)
x <- seq(0, 20, length.out = 101)
shape <- 3.5
scale <- 3
y <- x^(shape-1)*exp(-x/scale)/(scale^shape *gamma(shape))
plot(x, y)

yz <- dgamma(x, shape, scale=scale)
lines(x, yz, col = 'blue')

 

 

 

# 2-2. make a function and integrate it
f <- function(x,alpha,beta) {(x^(alpha-1)*exp(x/-beta))/(gamma(alpha)*beta^(alpha))}
a<- integrate(f,.5, 6, alpha=3.5, beta=3)

# 'dgamma' in R
b<- integrate(dgamma, .5, 6, shape=3.5 , scale=3)

a;b

---

3번) '삼중미분'을 실행하는 함수를 생성하고, "x^2 * y^4" 이 함수를 통해서 값을 확인함으로써 검증하세요

(특정 조건으로는 'D' 를 사용해도 좋고, 변수는 1~2개이면 좋다)

 

# Data ; 'f(x,y) = x^2 * y^4'
target <- expression(x^2*y^4)
"Original = x^2 * y^4" 

tri.der <- function(sm, num1, num2) {
    for (i in num1:0) {
      if(i==0) {break}
      sm <- D(sm,"x")
      if(i==1) {break}
    }
    
  for (j in num2:0) {
    if(j==0) {break} 
    sm <- D(sm,"y")
    if(j==1) {break}
  }
  sm
}
tri.der(target,0,3)
tri.der(target,1,2) 
tri.der(target,2,1)
tri.der(target,3,0)

 

 

---

4번) "Sign Test' 의 p-value 를 구하는 함수를 만들 것인데, 단 Q* = Q- = #(the number) of 'data < M0' 으로 설정하세요,

그리고, " DATA <- c(35,65,48,40,70,50,58,36,47,41,49,39,34,33,31), Mu zero=55 " 으로 주어질 것 입니다

 

library(DescTools)

DATA <- c(35,65,48,40,70,50,58,36,47,41,49,39,34,33,31)

sm <- function(x, muzero, side) {
  equal=0 ; low=0 ; high=0
  
  for (i in 1: length(x)) {
    if(x[i]==muzero) {equal=equal+1} 
    else if (x[i]<muzero) {low=low+1} 
    else {high= high+1} 
  }
  qstar.a <- low           ; qstar.c <- high
  qstar.b <- low+equal     ; qstar.d <- high+equal

  if (side=="two.sided") 
    {ifelse(low<high, pvalue <-(1- pbinom(qstar.b-1, length(x),0.5))*2, pvalue <- (1- pbinom(qstar.a-1, length(x),0.5))*2) }
  
  if (side=="less") 
    {pvalue <- 1-pbinom(qstar.a - 1, length(x), 0.5)}
  
  else if (side=="greater") 
  {pvalue <- pbinom(qstar.b , length(x), 0.5)}
  
  cat("\n",side ,"of Sign-Test","\np-value =",pvalue,
      "\nCompare with SignTest ft. in R =", SignTest(DATA, alternative = side, mu=muzero)$p.value)
}
sm(DATA, 55, "less")

 

 

 

---

<과제 총평>

1번 : 사실 필자가 적은 명령어에는 치명적인 오류가 있는데, '구간설정에서 두 변수를 뒤집었기 때문에, persp 를 형성할 때 x,z,y 와 각각 lim 구간이 서로 맞지 않음' 을 볼 수 있다.

이러한 문제점을 보기 싫다면 치환적분을 하는 것을 추천합니다 (치환하면 사실 엄청 쉬워집니다, 줄이 절반이 사라짐)

 

2번 : 눈치만 빠르다면, R내부에 있는 dgamma 에서 scale, shape parameter 가 각각 어떤 변수인지 감이 왔을 겁니다...

 

 

아직 감이 오지 않는다면, 다음 링크를 타고가서 해답을 알아보세요

https://m.blog.naver.com/PostView.nhn?blogId=parksehoon1971&logNo=220981033219&categoryNo=30&proxyReferer=https%3A%2F%2Fwww.google.co.kr%2F

[R Studio] 감마 분포(Gamma Distribution) plot 그리기

3번 : 삼중미분을 만들어내는 함수인데, 필자는 break 를 썼지만, 이해가 잘 안된다면 그냥 단순 노가다로 (if parameter=0 {} ...) 함수를 구성하셔도 됩니다...(그런데 이렇게 하면 사실상 하는 의미가...?)

 

4번 : 8차과제에서는 equal 데이터가 없었지만, equal 데이터가 존재할 경우도 생각해서 함수를 짜셔야해요, 그렇기 때문에 'Handling zeros' 에 대해서 정확하게 알고 있으셔야 합니다