전산통계학, 2019 중간고사

해당 답에 있는 이름은 지정되어 있는 답안이 아닌,

다양한 여러가지의 답들 중에 가장 깔끔한 답을 적어주셨던 당시의 선배님들 이름이니, 따로 크게 연연해하지 않으시길 바랍니다.

---

1번) 문제는 두 개입니다. (a),(b) 두 문제 모두 사진에서 확인된 모양의 원소를 '반드시 지정된 선에 대해서 대칭이 되도록!'교환하세요

(각각 5점씩)

# 1-(a)
x=matrix(1:121,11)

yj=function(x){
  for(j in 1:5){
    y<-x[(7-j):(5+j),j]
    x[(7-j):(5+j),j]<-x[(7-j):(5+j),(12-j)]
    x[(7-j):(5+j),(12-j)]<-y
  }
  x
}
yj(x)

---

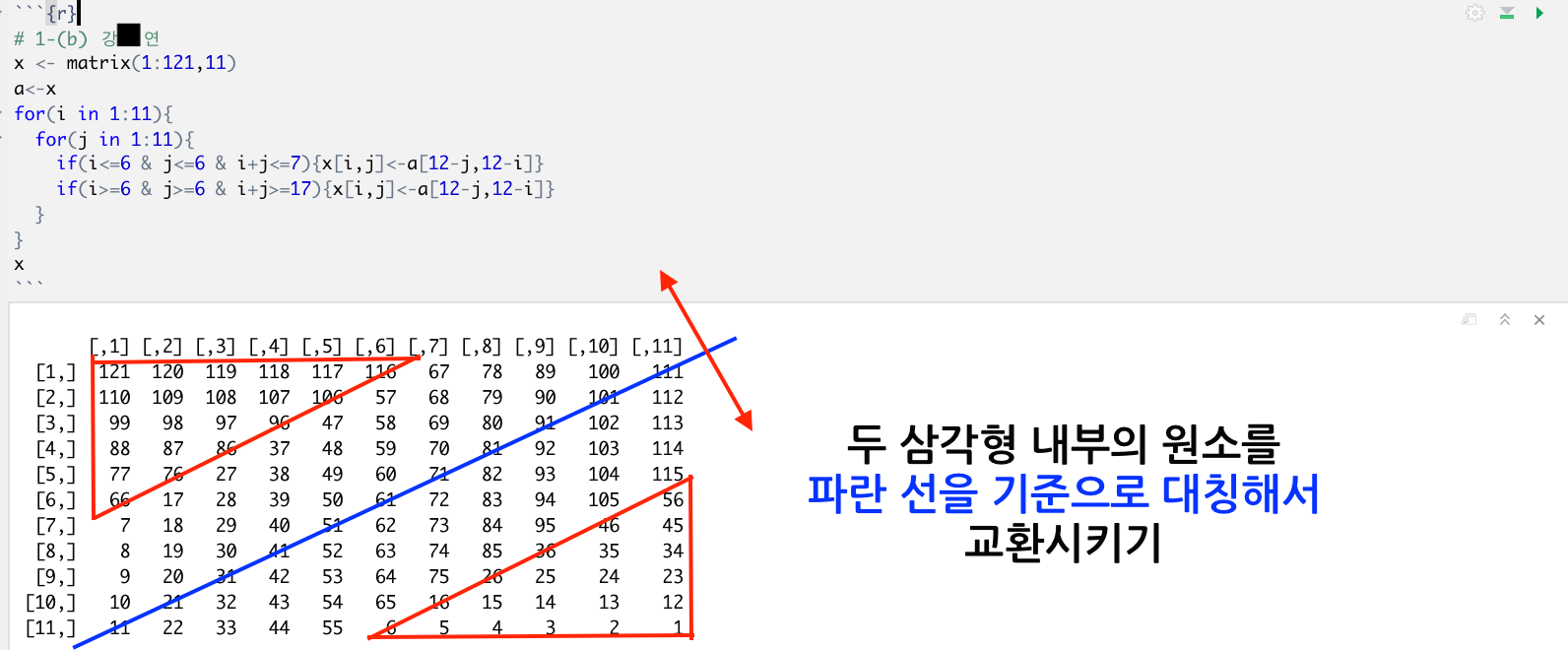
# 1-(b)
x <- matrix(1:121,11)
a<-x
for(i in 1:11){
  for(j in 1:11){
    if(i<=6 & j<=6 & i+j<=7){x[i,j]<-a[12-j,12-i]}
    if(i>=6 & j>=6 & i+j>=17){x[i,j]<-a[12-j,12-i]}
  }
}
x

---

2번) 문제는 두 개입니다. (a),(b) 두 문제 모두 지정된 순서나 규칙에 의거해서 array 꼴의 원소배열 (list 꼴) 이 나오도록 만드세요

(각각 5점)

# 2-(a)
x=1:24
yj.a=function(x,z1,z2,z3){
  y<-rep(0,length(x))
  dim(y)<-c(z1,z2,z3)
  for(i in 1:z3){
    y[,,z3-i+1]=matrix(x[z1*z2*i]:x[(i-1)*z1*z2+1],z1,z2,byrow=F)
  }
  y
}
yj.a(x,z1=2,z2=3,z3=4)

---

# 2-(b)
data=c(1:24)
sg=function(data){
  w=array(data,c(2,3,4))
  d=array(data,c(2,3,4))
  for(i in 1:dim(w)[1]){
    w[i,,]=d[3-i,,]}
  w
}
sg(data)

---

3번)  '바틀렛 검정 (Bartlett's test)' 에 대해서 프로그램을 짜세요, 원하는 결과의 값은 't.s & p-value' 이 두 가지 입니다 (5점)

# 3
y <- list()
y[[1]]<-c(1.51,1.92,1.08,2.04,2.14,1.76,1.17)

y[[2]]<-c(1.69,.64,.90,1.41,1.01,.84,1.28,1.59) 
y[[3]]<-c(1.56,1.22,1.32,1.39,1.33,1.54,1.04,2.25,1.49)
y[[4]]<-c(1.3,.75,1.26,.69,.62,.9,1.2,.32)

y[[5]] <- c(.73,.8,.9,1.24,.82,.72,.57,1.18,.54,1.3)

Btest <- function(y){
  k <- length(y) ; n <- c() ; S <- c() ; log10 <- c() ; Sp <- c()
  for(i in 1:k){
    n[i] <- length(y[[i]])
    N <- sum(n)
    S[i] <- sd(y[[i]])
    Sp2 <- sum((n-1)*S^2/(N-k))
    Q <- (N-k)*log10(Sp2)-sum((n-1)*log10(S^2))
    h <- 1 + (1/(3*(k-1)))*(sum((1/(n-1)-(1/(N-k)))))
    Bstar <- 2.3026*Q/h
    pvalue <- pchisq(Bstar,k-1,lower.tail = F)
  }
  list("B*"=Bstar,"P-value"=pvalue)
}
  
Btest(y)