미적분학 1-2. 함수의 극한

2. 함수의 극한

Maple 의 student 꾸러미에 들어있는 명령어 limit 를 사용하여 간단히 극한값을 구할 수 있다.

---

예제

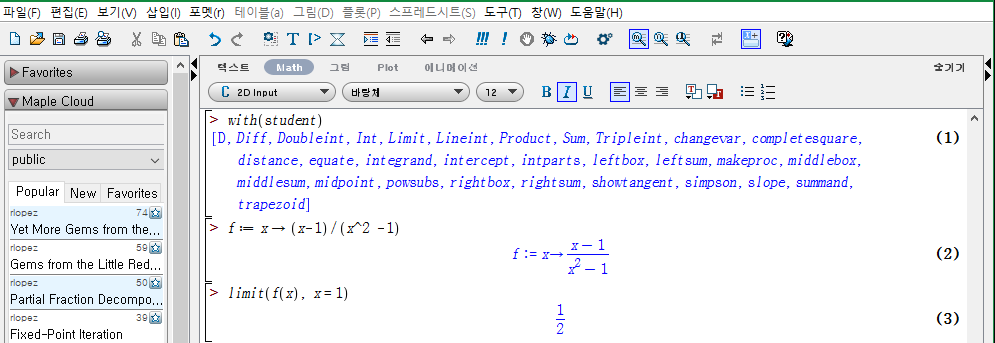
lim_(x->1) [ (x-1) / (x^2 -1) ] 의 값을 추측하여라.

 

with(student)

f:=x->(x-1)/(x^2 -1)

limit(f(x), x=1)

---

예제

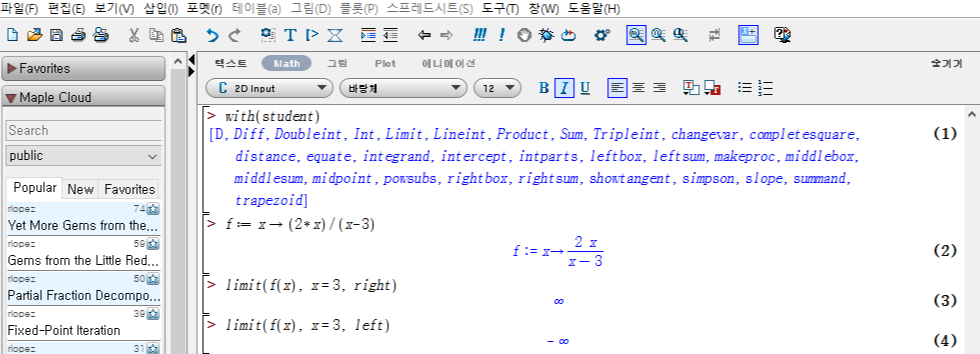
lim_(x->3+) [ 2x / (x-3) ] 와 lim_(x->3-) [ 2x / (x-3) ] 를 구하여라.

 

with(student)

f:=x->(2*x)/(x-3)

limit(f(x), x=3, right)

limit(f(x), x=3, left)

---

예제

lim_(x->0) (|x| / x) 은 존재하지 않음을 증명하여라.

 

with(student)

f:=x->abs(x)/x

limit(f(x), x=0, right)

limit(f(x), x=0, left)

---

예제

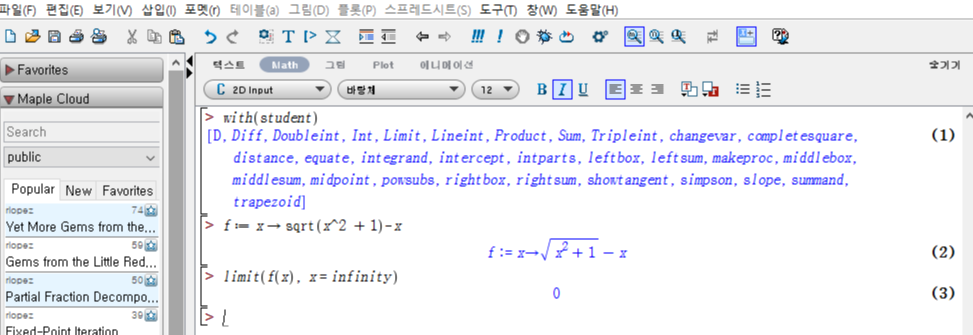
lim_(x->∞) [√(x^2+1)] -x 를 구하여라.

 

with(student)

f:=x->sqrt(x^2 +1)-x

limit(f(x), x=infinity)

---

직접해보기

함수 f의 그래프를 이용하여 값이 존재한다면 아래의 극한값을 구하여라. (존재하지 않는다면 그 이유를 보여라)

f(x)=1/ [1+ e^(1/x)]

 

다음 함수의 극한이 존재한다면 그 값을 구하여라.

lim_(t->-3) (t^2-9) / (2t^2 +7t +3)

 

다음 극한값을 구하거나 극한값이 존재하지 않음을 보여라.

lim_(t->∞) [(√t) + t^2] / (2t-t^2)