2020 전산통계학 5차 과제 - integral, uniroot, z-test

1번) R을 사용하여 다음 세 문제를 적분하시오

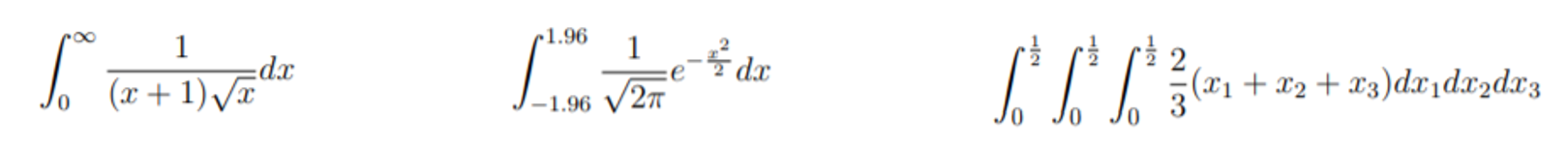
library(pracma)

# 1-(1)
f <- function(x) {1/ ((x+1)*sqrt(x) )}
integrate(f, lower=0, upper=Inf)$value

# 1-(2)
g <- function(x) {(1/sqrt(2*pi)*exp(-(x^2)/2))}
integrate(g, lower=-1.96, upper=1.96)$value

# 1-(3) ; tri integrate
sm <- function(x,y,z) {(2/3)*(x+y+z)}
integral3(sm, 0, .5, 0, .5, 0, .5)

---

2번) f(x)=-x^5-5x^3+9x^2-x-5 의 -3에서 3까지 그래프를 그려서 근의 위치를 대강 파악하고,
uniroot명령어를  사용하여 정확한 근을 구하시오

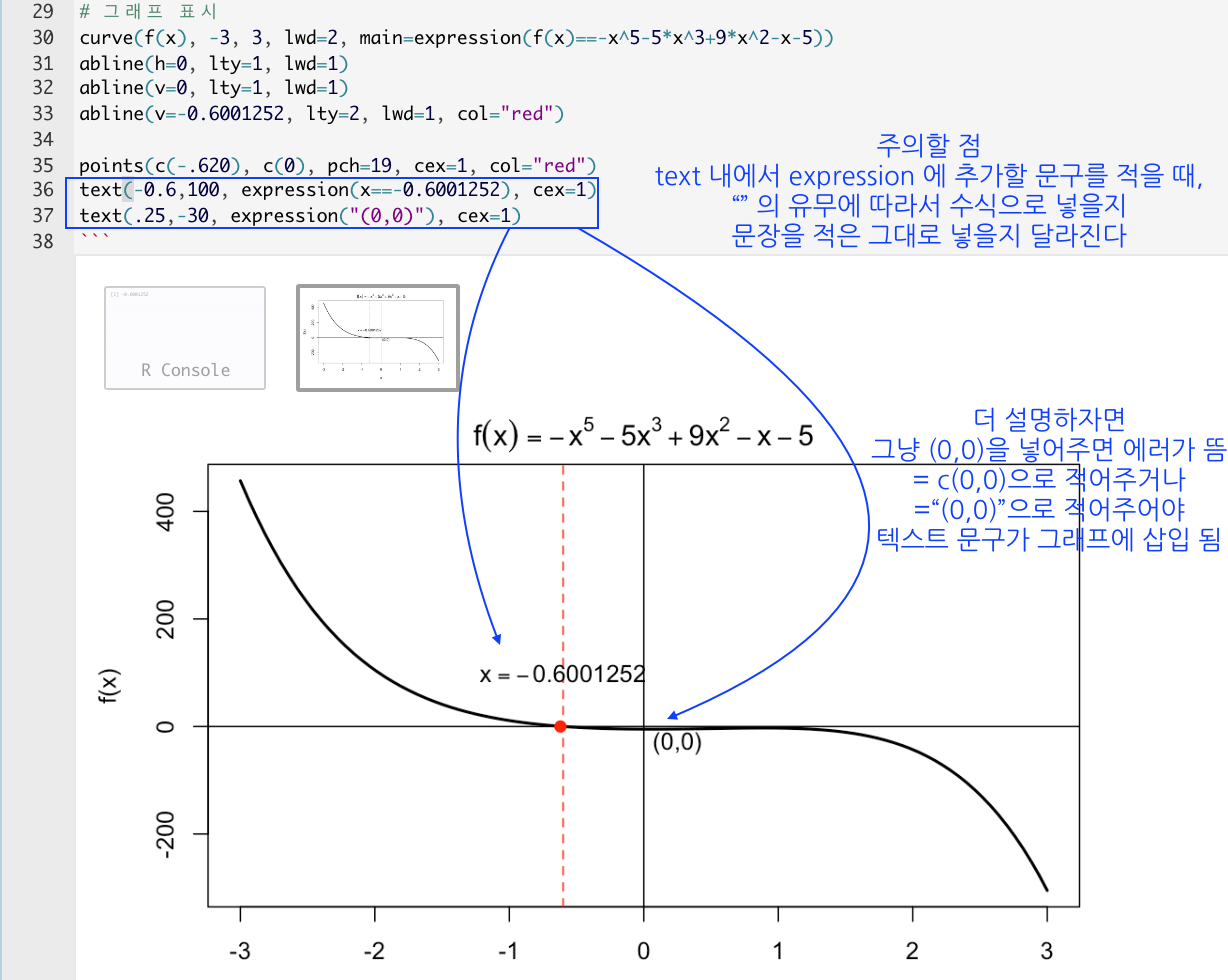
f <- function(x) {-x^5-5*x^3+9*x^2-x-5}

# -3~3 사이의 근 찾기
uniroot(f, c(-3, 3))$root

# 그래프 표시
curve(f(x), -3, 3, lwd=2, main=expression(f(x)==-x^5-5*x^3+9*x^2-x-5))
abline(h=0, lty=1, lwd=1)
abline(v=0, lty=1, lwd=1)
abline(v=-0.6001252, lty=2, lwd=1, col="red")

points(c(-.620), c(0), pch=19, cex=1, col="red")
text(-0.6,100, expression(x==-0.6001252), cex=1)
text(.25,-30, expression("(0,0)"), cex=1)

---

3번) BSDA 패키지 내에 있는 z.test 명령어를 사용하여 구한 two-sample z test 결과입니다. z검정을 할 때 배웠던 수식들을 사용하여 검정색 글씨부분과 똑같은 결과를 만드는 프로그램을 만드시오
(데이터_1, 데이터_2, σ_1, σ_2, aplpha(conf_level : 유의 수준) 들을 변수로 사용하시오)

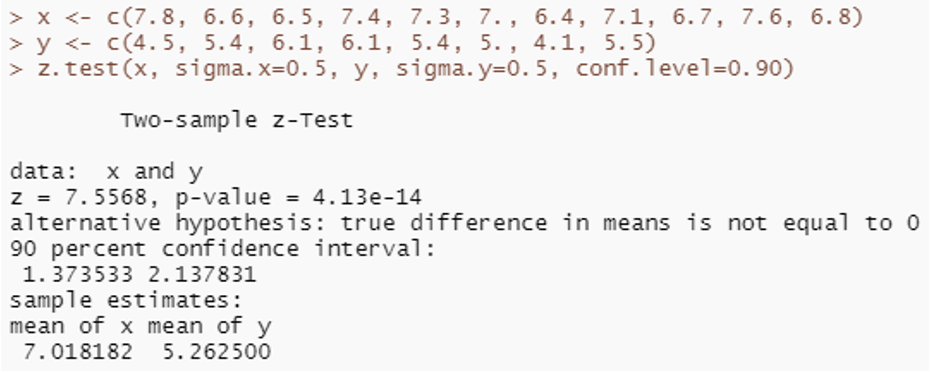
library(BSDA)

x <- c(7.8, 6.6, 6.5, 7.4, 7.3, 7.0, 6.4, 7.1, 6.7, 7.6, 6.8)
y <- c(4.5, 5.4, 6.1, 6.1, 5.4, 5.0, 4.1, 5.5)

 

 

# make f.t
smz <- function (data1, data2, sigma1, sigma2, conflevel) {
  
  # z_statistic
  zstat <- ((mean(data1)-mean(data2)) - (0-0))/sqrt(((sigma1)^2/length(data1)+((sigma2)^2)/length(data2)))
  
  # p-value
  ifelse(zstat<0, pvalue <- 1-pnorm(zstat, lower.tail = T),
  pvalue <- pnorm(zstat, lower.tail = F))
  pvalue <- pvalue*2
  
  # C.I
  ub <- (mean(data1)-mean(data2)) - qnorm((1-conflevel)/2)*sqrt(((sigma1)^2/length(data1)+((sigma2)^2)/length(data2)))
  lb <- (mean(data1)-mean(data2)) + qnorm((1-conflevel)/2)*sqrt(((sigma1)^2/length(data1)+((sigma2)^2)/length(data2)))

  # result (hypohersis)
  result <- "alternative hypothesis: true difference in means is not equal to 0"
  
  # make sentence equal to z.test (in R)
  cat("\n        Two Sample z-test\n\ndata:  x and y \nz = ",round(zstat,4),", p-value = ",pvalue ,
      "\n",result ,"\n", (conflevel)*100 , " percent confidence interval:\n ", lb," ",ub, 
      "\n", "sample estimates:\nmean of x mean of y \n", " ",mean(x),"  ", mean(y) , sep = "")
}

z.test(x, sigma.x=.5, y, sigma.y=.5, conf.level = .9) ; smz(x,y,0.5, 0.5, 0.9)

---

<과제 총평>

1번 : 지금은 친절하게 적분구간을 제시해주었기 때문에 매우 쉽지만, 보통은 적분구간까지 직접 찾아서 해봐야하는 문제가 많이 나옴
그 예시로 2019 전산통계학 기말고사 당시 1번 문제처럼 주어지는 경우 : smbar.tistory.com/72?category=814595

전산통계학, 2019 기말고사

 

2번 : 일반적으로 plot을 잘 다룬다면 그래프 표시, 그래프 추가 같은 2번 문제는 쉬움

 

3번 : "R 내부의 함수가 있는데 뭐하러 고생해서 이 결과랑 똑같이 만드냐?" 라는 생각을 할 수 있겠지만, 오히려 그 함수를 만드는 과정에서 각 test에 쓰이는 수식이나 알고리즘이 의외로 머릿속에서 강하게 남아있음;; 도움이 많이 되는 유형의 과제임
그런데 이번 3번 문제에서 주의해야 할 점은  # result (hypohersis) 이 부분

원래대로라면, 지금은 결론을 아예 "alternative hypothesis: true difference in means is not equal to 0"" 로 고정해버렸지만 두 개의 결론으로 ifelse 같은 조건문을 사용하여 나누어 주는 것이 옳습니다. (직접 생각해봅시다) 또한 변수에 μ_0 또한 주어져서 "~equal to", μ_0 와 같이 설정해주는 것이 올바른 프로그램 구조