전산통계학, 2019 기말고사

해당 답에 있는 이름은 지정되어 있는 답안이 아닌,

다양한 여러가지의 답들 중에 가장 깔끔한 답을 적어주셨던 당시의 선배님들 이름이니, 따로 크게 연연해하지 않으시길 바랍니다.

---

1번) 지정한 영역에 대해서 삼중적분을 실행한 값을 구하세요, f:x*y^2*z^3 ,C:0<x<y<z<1 (5점)

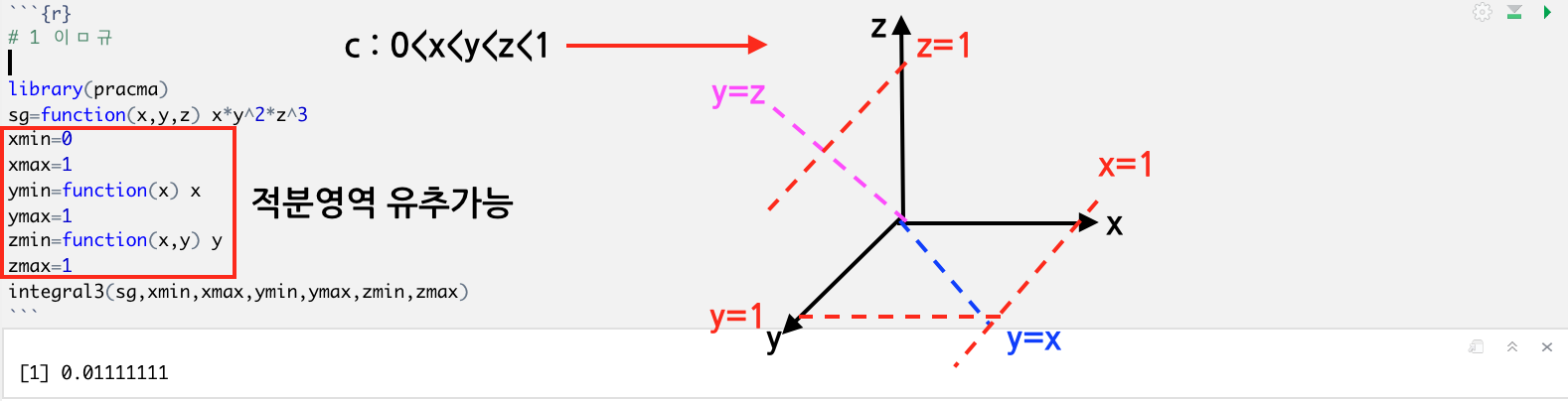
# 1
library(pracma)

sg=function(x,y,z) x*y^2*z^3
xmin=0
xmax=1
ymin=function(x) x
ymax=1
zmin=function(x,y) y
zmax=1

integral3(sg,xmin,xmax,ymin,ymax,zmin,zmax)

---

2번) 교재의 주어진 데이터를 이용해서 "y=Beta0 + Beta1*x (x : fixed)" 에 대해서 x=1.7 일 때의 다음 값들을 구하세요 (5점)

(beta 0 , beta 1, s^2, "C.I for y=Beta0 + Beta1*(1.7)", "C.I for Y|x=1.7") 이 값들을 프로그래밍의 값으로만 나오게 하면 됩니다

# 2
x=c(1.35,1.9,1.7,1.8,1.3,2.05,1.6,1.8,1.85,1.4)
y=c(17.9,16.5,16.4,16.8,18.8,15.5,17.5,16.4,15.9,18.3)
#beta0+beta1x (x:fixed) - CI
yj=function(x,alpha,x0){
  n=length(x)
  sxx=sum((x-mean(x))^2)
  b1=((n*sum(x*y))-(sum(x)*sum(y)))/(n*sum(x^2)-(sum(x))^2)
  b0=mean(y)-b1*mean(x)
  syy=sum((y-mean(y))^2)
  sxy=sum(x*y)-n*mean(x)*mean(y)
  sse=syy-b1*sxy
  s2=sse/(n-2)
  s=sqrt(s2)
  df=n-2
  
  L1=(b0+b1*x0)-qt(alpha/2,df,lower.tail = F)*s*sqrt(1/n+((x0-mean(x))^2)/sxx)
  L2=(b0+b1*x0)+qt(alpha/2,df,lower.tail = F)*s*sqrt(1/n+((x0-mean(x))^2)/sxx)
  CI=c(L1,L2)
  
  L3=(b0+b1*x0)-qt(alpha/2,df,lower.tail = F)*s*sqrt(1/n+((x0-mean(x))^2)/sxx+1)
  L4=(b0+b1*x0)+qt(alpha/2,df,lower.tail = F)*s*sqrt(1/n+((x0-mean(x))^2)/sxx+1)
  PI=c(L3,L4)
  
  cat("b0=",b0,"b1=",b1,"s^2=",s2,"CI for beta0+beta1*1.7=",CI,"CI for Y|x=1.7",PI)
}
yj(x,0.1,1.7)

---

3번) 문제는 두 개입니다

(a). 주어진 데이터를 이용해서 "Friedman Test" 를 직접 코딩하여서 p-값을 도출하고, "aov (R 자체함수)" 를 이용해서 p-값을 도출하세요, 따라서 두 개의 p-값을 구하면 됩니다 (7점)

(b). 위에서 구한 "p-값(Friedman) 에서 p-값(aov) 을 뺀 값"을 구하세요 (3점)

# 3
x<-c(9.1,13.4,15.6,11.0,12.7,
     17.1,20.3,24.6,18.2,19.8,
     20.8,28.3,23.7,21.4,25.1,
     11.8,16.0,16.2,14.1,15.8)
A<-gl(4,5)
B<-factor(rep(1:5,len=20))
Sj<-function(x){
  a<-length(levels(A))
  b<-length(levels(B))
  n<-length(x)
  s<-c();g<-matrix(nrow=b,ncol=a);m<-c()
  s<-tapply(x,B,rank)
  for(i in 1:b){
    for(j in 1:a){
      g[i,j]<-s[[i]][j] 
    }
  }
  m<-apply(g,2,sum)
  sstar<-(12/(b*a*(a+1)))*sum(m^2)-3*b*(a+1)
  pvalue1<-pchisq(sstar,(a-1),lower.tail = F)
  pvalue2<-summary(aov(x~A+B))[[1]][[5]][[1]]
  cat("pvalue1(friedman test) is",pvalue1,"pvalue2(aov) is ",pvalue2,"\n So pvalue1 - pvalue2 is ",pvalue1-pvalue2)
}
Sj(x)

---

4번) 제시된 categorical 데이터를 'chi-squared goodness test' 혹은 'independent test' 혹은 'homogeneity' 중에서 올바른 테스트를 통해 p-값을 도출하세요 (5점)

# 4
# DATA
data <- matrix(c(75, 160, 100, 15, 60, 115, 65, 10, 65, 175, 135, 25), nrow = 4, byrow = F,
               dimnames = list("Injury" = c("None", "Minor", "Major", "Death"),
                                "Restraint" = c("seat belt","both", "None")) )

indi <- function (x) {
  r <-nrow(x) ; c <- ncol(x)
  
  # df
  df <- (r-1)*(c-1)
  ni. <- c() ; n.j <- c()
  for (i in 1:r) {ni.[i] <- sum(x[i,])}
  for (j in 1:c) {n.j[j] <- sum(x[,j])}
  
  # expected
  E <- matrix(nr=r, nc=c)
  for (i in 1:r) {
    for (j in 1:c) {
      E[i,j] <- (ni.[i]*n.j[j])/sum(x)
    }
  }
  # t.s
  su <- 0
  for (i in 1:r) {
    for (j in 1:c) {
      su <- su+ (x[i,j]-E[i,j])^2 /E[i,j]
    }
  }
  chistar <- sum(su)
  pv <- pchisq(chistar,df=df,lower.tail = F)
  cat ("p-value =",pv)
}
indi(data)