전산통계학 3차 과제 - 이분산가정(p값 도출), 등분산가정(p값 도출), T 테스트
코딩 공부/R-전산 통계학 2019. 11. 19. 22:061번) x1<-c(246.3, 255.0, 245.8, 250.7, 247.7, 246.3, 214.0, 242.7, 287.5, 284.6, 268.7, 302.6, 248.3, 243.7, 276.7, 254.9)
x2<-c(340.7, 270.1, 371.6, 306.6, 263.4, 341.6, 307.0, 319.1, 272.6, 332.6, 362.2, 358.1, 271.4, 303.9, 324.7, 360.1)
위의 두 데이터를 통해서 '이분산' 가정일 경우의 p-value 를 모든 사이드에 따라서 값이 출력되게끔 함수를 만들기
(단! test statistic 과 degree of freedom 을 정의하는 함수를 만들어서, 최종 함수 안에 두 함수를 넣는 형태로 만드세요)
#Data
x1<-c(246.3, 255.0, 245.8, 250.7, 247.7, 246.3, 214.0, 242.7, 287.5, 284.6, 268.7, 302.6, 248.3, 243.7, 276.7, 254.9)
x2<-c(340.7, 270.1, 371.6, 306.6, 263.4, 341.6, 307.0, 319.1, 272.6, 332.6, 362.2, 358.1, 271.4, 303.9, 324.7, 360.1)
n1=length(x1) ; n2=length(x2)
s1=var(x1) ; s2=var(x2)
# 1st; make t test statistic
tstar <- function(x1,x2,l) {
tstar <- (mean(x1)-mean(x2)-l)/sqrt(s1/n1+s2/n2)
tstar
}
tstar(x1,x2,0)
# 2nd; make the degree of freedom <- not use 'floor', because we get a specific p.value
df <- function(x1,x2) {
r <- (s1/n1+s2/n2)^2/(((s1/n1)^2)/(n1-1)+((s2/n2)^2)/(n2-1))
r
}
df(x1,x2)
# 3rd; use two function , make the p-value function
pvalue <- function(tstar,df,sided){
r <- df(x1,x2)
if(sided=="two.sided") {
ifelse(tstar > 0 , pva.<-pt(tstar,r,lower.tail = F)*2, pva.<-pt(tstar,r)*2)
}
if(sided=="less") {
pva.<-pt(tstar,r)
}
if(sided=="greater") {
pva.<-pt(tstar,r,lower.tail = F)
}
print(pva.)
}
all.equal(t.test(x1,x2,"two.sided")$p.value, pvalue(tstar(x1,x2,0),df(x1,x2),"two.sided"))
all.equal(t.test(x1,x2,"less")$p.value, pvalue(tstar(x1,x2,0),df(x1,x2),"less"))
all.equal(t.test(x1,x2,"greater")$p.value,pvalue(tstar(x1,x2,0),df(x1,x2),"greater"))

2번) 위에서 수행한 '1번 문제' 를 '등분산' 가정일 경우의 p-value 값을 출력하는 함수를 만들기 (함수 안에 함수 넣기 조건도 동일)
y1<-c(246.3, 255.0, 245.8, 250.7, 247.7, 246.3, 214.0, 242.7, 287.5, 284.6, 268.7, 302.6, 248.3, 243.7, 276.7, 254.9)
y2<-c(340.7, 270.1, 371.6, 306.6, 263.4, 341.6, 307.0, 319.1, 272.6, 332.6, 362.2, 358.1, 271.4, 303.9, 324.7, 360.1)
n1=length(y1) ; n2=length(y2)
s1=var(y1) ; s2=var(y2)
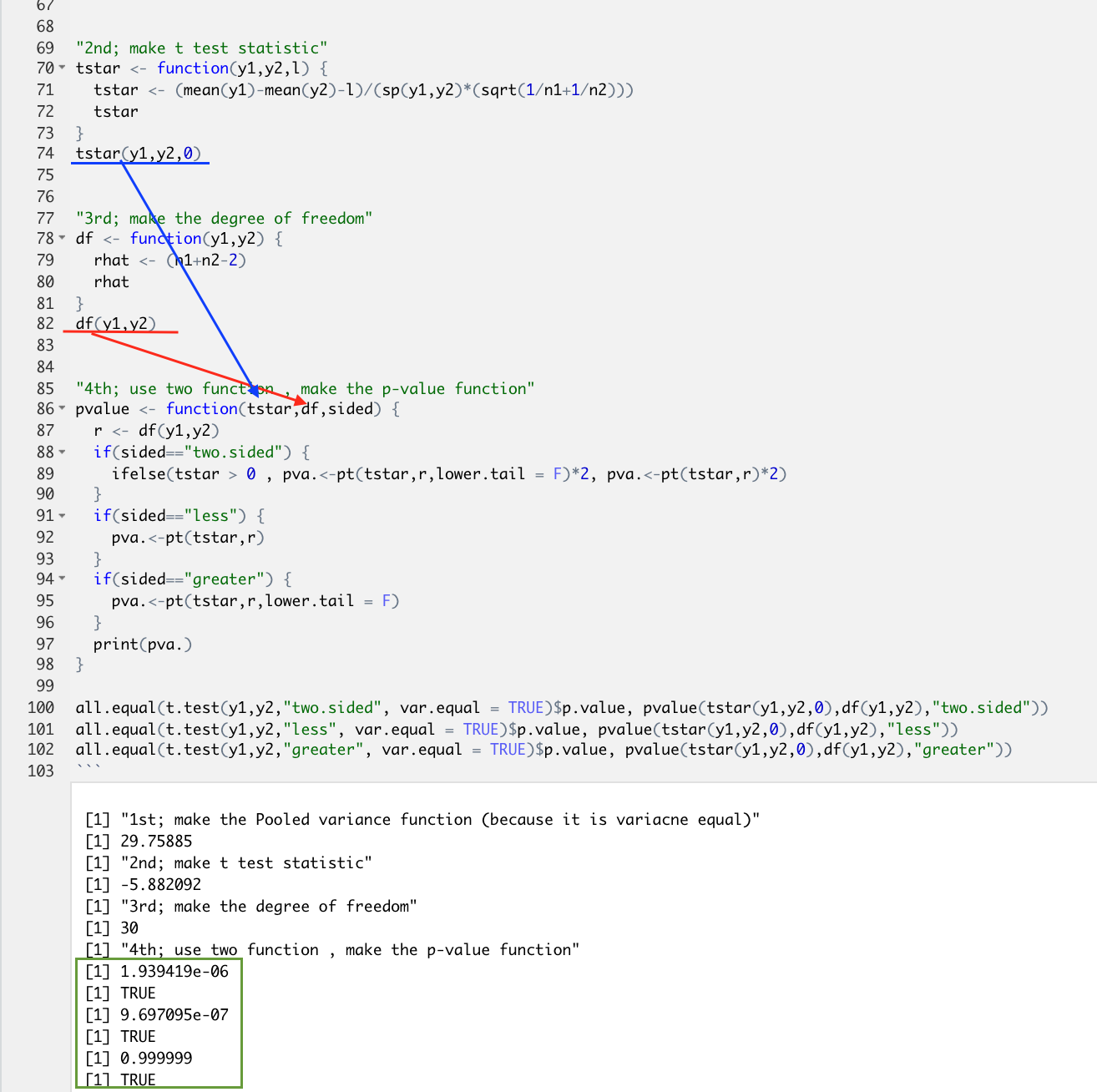
# 1st; make the Pooled variance function (because it is variacne equal)
sp <- function(y1,y2) {
sp <- ((n1-1)*s1+ (n2-1)*s2) / (n1+n2-2)
sqrt(sp)
}
sp(y1,y2)
# 2nd; make t test statistic
tstar <- function(y1,y2,l) {
tstar <- (mean(y1)-mean(y2)-l)/(sp(y1,y2)*(sqrt(1/n1+1/n2)))
tstar
}
tstar(y1,y2,0)
# 3rd; make the degree of freedom
df <- function(y1,y2) {
rhat <- (n1+n2-2)
rhat
}
df(y1,y2)
# 4th; use two function , make the p-value function
pvalue <- function(tstar,df,sided) {
r <- df(y1,y2)
if(sided=="two.sided") {
ifelse(tstar > 0 , pva.<-pt(tstar,r,lower.tail = F)*2, pva.<-pt(tstar,r)*2)
}
if(sided=="less") {
pva.<-pt(tstar,r)
}
if(sided=="greater") {
pva.<-pt(tstar,r,lower.tail = F)
}
print(pva.)
}
all.equal(t.test(y1,y2,"two.sided", var.equal = TRUE)$p.value, pvalue(tstar(y1,y2,0),df(y1,y2),"two.sided"))
all.equal(t.test(y1,y2,"less", var.equal = TRUE)$p.value, pvalue(tstar(y1,y2,0),df(y1,y2),"less"))
all.equal(t.test(y1,y2,"greater", var.equal = TRUE)$p.value, pvalue(tstar(y1,y2,0),df(y1,y2),"greater"))
3번) x<-c(246.3, 255.0, 245.8, 250.7, 247.7, 246.3, 214.0, 242.7, 287.5, 284.6, 268.7, 302.6, 248.3, 243.7, 276.7, 254.9)
y<-c(340.7, 270.1, 371.6, 306.6, 263.4, 341.6, 307.0, 319.1, 272.6, 332.6, 362.2, 358.1, 271.4, 303.9, 324.7, 360.1)
위의 데이터를 통해서 R안의 함수인 't.test' 를 사용해서 나오는 함수값과 동일한 값을 가지게 하는 함수 만들기 (참고로, var.equal = T)
x<-c(246.3, 255.0, 245.8, 250.7, 247.7, 246.3, 214.0, 242.7, 287.5, 284.6, 268.7, 302.6, 248.3, 243.7, 276.7, 254.9)
y<-c(340.7, 270.1, 371.6, 306.6, 263.4, 341.6, 307.0, 319.1, 272.6, 332.6, 362.2, 358.1, 271.4, 303.9, 324.7, 360.1)
sm<-function(x,y,mu,sided,alpha) {
n1=length(x) ; n2=length(y)
s1=var(x) ; s2=var(y)
Sp <- sqrt( ( ((n1-1)*s1+ (n2-1)*s2) / (n1+n2-2) ) )
tstar<-(mean(x)-mean(y)-mu)/(Sp*(sqrt(1/n1+1/n2)))
df<-(n1+n2-2)
if(sided=="two.sided") {
ifelse(tstar > 0 , pvaue<-pt(tstar,df,lower.tail = F)*2, pvalue<-pt(tstar,df)*2)
result <- c("alternative hypothesis: true difference in means is not equal to ", mu)
L1<- ( (mean(x)-mean(y))+ qt(0.5-alpha/2, df)*(Sp * sqrt(1/n1+1/n2)) ) ; L2<- ( (mean(x)-mean(y))+ qt(0.5-alpha/2, df, lower.tail = F)*(Sp * sqrt(1/n1+1/n2)) )
}
if(sided=="less") {
pvalue <- pt(tstar,df)
result <- c("alternative hypothesis: true difference in means is less than ", mu)
L1<-" -Inf" ; L2<- ( (mean(x)-mean(y))+ qt(alpha, df)*(Sp * sqrt(1/n1+1/n2)) )
}
if(sided=="greater") {
pvalue <- pt(tstar,df, lower.tail = F)
result <- c("alternative hypothesis: true difference in means is greater than ", mu)
L1<- ( (mean(x)-mean(y))+ qt(1-alpha, df)*(Sp * sqrt(1/n1+1/n2)) ) ; L2<- " Inf"
}
cat("\n Two Sample t-test\n\ndata: x and y \nt = ",round(tstar,4),", df = ",df,", p-value = ",pvalue ,
"\n",result ,"\n", (alpha)*100 , " percent confidence interval:\n ", L1," ",L2,
"\n", "sample estimates:\nmean of x mean of y \n", " ",mean(x)," ", mean(y) , sep = "")
}
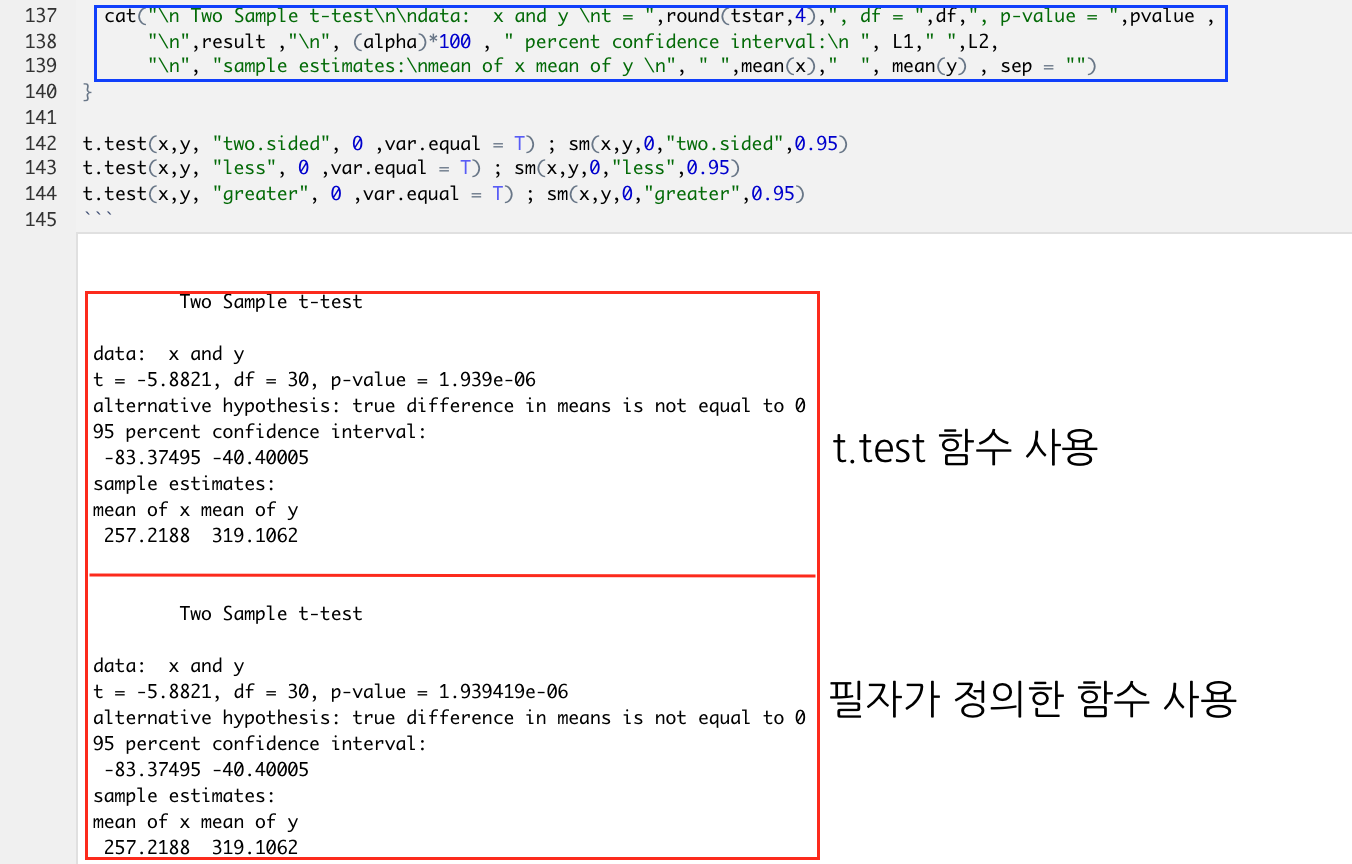
t.test(x,y, "two.sided", 0 ,var.equal = T) ; sm(x,y,0,"two.sided",0.95)
t.test(x,y, "less", 0 ,var.equal = T) ; sm(x,y,0,"less",0.95)
t.test(x,y, "greater", 0 ,var.equal = T) ; sm(x,y,0,"greater",0.95)
<과제 총평>
1번 : 이분산 가정일 때의 p-value 값 도출 과정을 잘 이해한다면 쉬웠을 거에요
2번 : 등분산 가정은 이분산과 달리, Sp 라는 값이 추가로 정의되고, d.f 를 찾는 방법이 다름만 안다면야...
3번 : 반복적인 공백 (빈 칸) 노가다와 cat 노가다를 많이 하면, 어렵지는 않았을 거라고 생각되요
추가로 조언해 드리자면, 어떤 사람들은 "공백이 knit 돌렸을 때와 다르게 나와요!" 라고 하는 분들도 조금씩 계셨는데, 공백을 스페이스 바로 하지 말고, cut and paste 해서 하는 것이 더 정확하게 나옵니다
 TAG
TAG






