전산통계학 6차 과제 - T 테스트, RCD ANOVA, Latin square

1번) 'Paired T-Test' function 만들기 (R 내의 명령어인 t.test 와 값, 띄어쓰기도 동일하게 나와야 합니다)

데이터는 ''351p. example 10.5.2" 로 이용하세요

#Data

x=c(8.05,24.74,28.33,8.45,9.19,25.2,14.05,20.33,4.82,8.54)
y=c(.71,.74,.74,.77,.8,.83,.82,.77,.71,.72)

paired<-function(x,y,mu,sided,alpha) { 
d=(x-y)
n<-length(d)
Sd<-sqrt(var(d))
tstar<-(mean(d)-mu) / (Sd/sqrt(n))
df<-(n-1)

  if(sided=="two.sided") { 
    ifelse(tstar > 0 , bf.pvalue<-pt(tstar,df,lower.tail = F)*2, bf.pvalue<-pt(tstar,df)*2)
    pvalue<- round(bf.pvalue,7)
    result <- c("alternative hypothesis: true difference in means is not equal to ", mu)
    L1<- (mean(d) + qt(0.5-alpha/2, df)*(Sd/sqrt(n) )) ; L2<- (mean(d) + qt(0.5-alpha/2, df, lower.tail = F)*(Sd/sqrt(n) ))
  }
  
  if(sided=="less") {
    bf.pvalue <- pt(tstar,df)
    pvalue<-round(bf.pvalue,4)
    result <- c("alternative hypothesis: true difference in means is less than ", mu)
    L1<-"    -Inf" ; L2<- ( mean(d)+ qt(alpha, df)*(Sd/sqrt(n)) )
  }
  
  if(sided=="greater") {
    bf.pvalue <- pt(tstar,df, lower.tail = F)
    pvalue<-round(bf.pvalue,7)
    result <- c("alternative hypothesis: true difference in means is greater than ", mu)
    L1<-( mean(d)+ qt(1-alpha, df)*(Sd/sqrt(n) )) ; L2<- "     Inf"
  }
  
  cat("\n Paired t-test\n\ndata:  x and y \nt = ",round(tstar,4),", df = ",df,", p-value = ",pvalue ,
      "\n",result ,"\n", (alpha)*100 , " percent confidence interval:\n",ifelse(sided=='two.sided',"  "," "), L1," ",L2, 
      "\n", "sample estimates:\nmean of the differences \n", "                 ",mean(d) , sep = "")
}

t.test(x,y, "two.sided" ,mu=0, TRUE) ; paired(x,y,0,"two.sided",0.95)
t.test(x,y, "less" ,mu=0, TRUE) ; paired(x,y,0,"less",0.95)
t.test(x,y, "greater" ,mu=0, TRUE) ; paired(x,y,0,"greater",0.95)

---

2번) R.C.D (Randomized Complete Design) 의 ANOVA table 에 관한 프로그램 짜기 (print 할 항목 = table, F*, p-value 입니다)

데이터는 ''514p. example 13.1.2" 로 이용하세요

# Data

y=list()
y[[1]]<-c(1.51, 1.92, 1.08, 2.04, 2.14, 1.76, 1.17)
y[[2]]<-c(1.69, 0.64, 0.90, 1.41, 1.01, 0.84, 1.28, 1.59)
y[[3]]<-c(1.56, 1.22, 1.32, 1.39, 1.33, 1.54, 1.04, 2.25, 1.49)
y[[4]]<-c(1.30, 0.75, 1.26, 0.69, 0.62, 0.90, 1.20, 0.32)
y[[5]]<-c(0.73, 0.80, 0.90, 1.24, 0.82, 0.72, 0.57, 1.18, 0.54, 1.30)


smanova<-function(y) {
  k<-length(y)
  n<-c()
  t<-c()

 

이 다음부터는 필자가 데이터를 list 형태로 주었기 때문에, 각 k에 대한 길이 (=해당하는 원소의 개수) 나, sum 을 이런식으로 규정할 것이기 때문에 이해하는데 조금 짜증날 것입니다...

  for (i in 1:k) {
    n[i] <- length (y[[i]]) 
    t[i] <- sum(y[[i]])
  }
  
  N<-sum(n)
  t..<-sum(t)
  tn<-c()
  
  
  # Sum Square
  for (i in 1:k) {
   tn[i]<- sum(t[i]^2/n[i])
  }
  sstrt<-sum(tn)-(t..^2)/N
  
  
  yij<-0
  
  for (i in 1:k) {
    for (j in 1:n[i]) {
      yij<-yij+(y[[i]][j])^2
    }
    yij
  }
  sstot <- yij-(t..^2)/N
  sse <- sstot-sstrt

  
  # Mean Square
  mstrt <- sstrt/(k-1)
  mse   <- sse/(N-k)
  
  
  # F.star & P-value
  fstar <- (mstrt/mse)
  pvalue <- pf(fstar, (k-1), (N-k), lower.tail = F)


  # ANOVA Table
  table <- matrix(c(k-1, N-k, N-1,
                    sstrt, sse, sstot,
                    mstrt, mse, NA
                    ,fstar,NA ,NA ), nrow = 3, ncol = 4, dimnames = list(c("Treatment","Error","Total"), c("D.F", "S.S", "M.S", "F*")) )
  
  
 result <- list(table,fstar,pvalue)
 names(result) <- c("ANOVA Table","F*","p-value")
 result
}

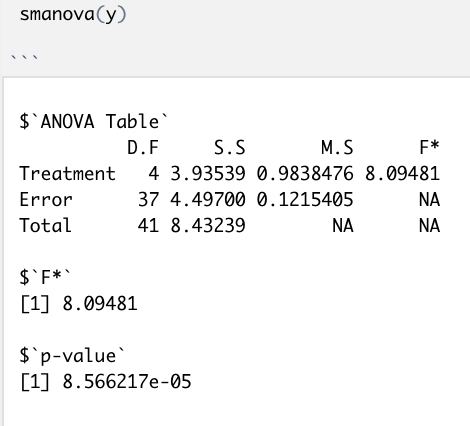
 smanova(y)

---

3번) Latin Square 에 관한 프로그램 짜기 (print 할 항목 = F*, p-value 입니다)

데이터는 ''566p. table 13.12" 로 이용하세요

# Data 
x<-matrix (c(3, 1, 4.5, 5.5, 4.2, 5.6, 3.5, .8, .9, 3.8, 5.7, 3.9, 5.3, 4.3, 1.2, 3.7) ,4)

reallatin<-function(x) {
t...<-sum(x)
r<- nrow(x)

sstotal<-sum(x^2)-(t...^2/(r^2))

# Sum Square
trt<-c(1,3,2,4,2,4,1,3,3,1,4,2,4,2,3,1)
trt<-factor(trt)
Ti..<-tapply(x,trt,sum)
sstrt<- sum(Ti..^2/r)-(t...^2/(r^2))

 

강의에서 언급했던 factor 가 Latin 의 데이터 분류를 하는 데, 큰 도움을 줍니다

col<-gl(4,4)
row<-factor(rep(1:4,4))

T.j.<-tapply(x,row,sum)
ssrow<-sum(T.j.^2/r)-(t...^2/(r^2))
T..k<-tapply(x,col,sum)
sscol<-sum(T..k^2/r)-(t...^2/(r^2))

sserror<-sstotal-(sstrt+ssrow+sscol)

# Mean Square
 mstrt<-sstrt/(r-1)
  msrow<-ssrow/(r-1)
  mscol<-sscol/(r-1)
  mserror<-sserror/((r-1)*(r-2))
  
  # F.star & P-value
  f1star <- mstrt/mserror
  pvalue1 <- pf(f1star, (r-1), (r-1)*(r-2), lower.tail = F)
  
  
 result <- list(f1star,pvalue1)
 names(result) <- c("F*","p-value")
 result
}
reallatin(x)

---

<과제 총평>

1번 : 지난 과제에서 한 것처럼, 빈칸 노가다와 round (내림) 을 이용해서 결과값을 조정하는 문제

 

2번 : R.C.D 에서 F* 를 도출해내는 원리만 이해하고 있다면, 어렵지는 않을 듯 싶으나... 데이터 구조에서 k 에 따른 길이, 합을 뽑아내는 것이 조금 까다로웠던 것으로 생각되요...

그래서 어떤 사람은 이런식으로도 데이터구조를 짰으니, 한 번 참고하셔도 좋을 것 같습니다

 

3번 : Latin Square 에서 데이터의 분류는 총 3가지인데, factor 을 여기서 잘 이용해 먹읍시다... 

(중간고사 이후에, 또 쓸 예정이니 잘 기억해두고 그때도 잘 이용합시다)