R, Post Hoc program example (14' KTS)

# Bonferroni

y <- c(1.51,1.92,1.08,2.04,2.14,1.76,1.17
       ,1.69,0.64,0.90,1.41,1.01,0.84,1.28,1.59
       ,1.56,1.22,1.32,1.39,1.33,1.54,1.04,2.25,1.49
       ,1.30,0.75,1.26,0.69,0.62,0.90,1.20,0.32
       ,0.73,0.80,0.90,1.24,0.82,0.72,0.57,1.18,0.54,1.30)
x <- as.factor(rep(1:5,c(7,8,9,8,10)))


bonferroni.func <- function(y,x,alpha=0.05){
  n <- length(y); k <- nlevels(x); df <- n-k
  model <- aov(y~x)
  
  MSE <- deviance(model)/(n-k)
  
  mean.i <- tapply(y,x,mean)
  n.i <- tapply(y,x,length)
  
  raw.dat <- cbind(mean.i,n.i)
  
  sm <- raw.dat[order(mean.i),1]
  sn.i <- raw.dat[order(mean.i),2]
  
  name.vec <- as.numeric(names(sm))
 

  # number of tests
  c <- sum(1:k)
  b.t <- qt(1-alpha/(2*c),df)
  
  reject <- upper <- lower  <- name.dun <- difference <- c()
  
  for(i in 1:(k-1)){
    for(j in k:2){
      if(j>i){
        dif <- sm[i]-sm[j]
        difference <- c(difference,abs(dif))
        name.dun <- c(name.dun,paste(name.vec[i],"-",name.vec[j],sep=""))
        u <- dif+b.t*sqrt(MSE*(1/sn.i[i]+1/sn.i[j])); upper <- c(upper,u)
        l <- dif-b.t*sqrt(MSE*(1/sn.i[i]+1/sn.i[j])); lower <- c(lower,l)
        reject <- c(reject,ifelse(0>l&0<u,"no","yes"))
      }
    }
  }

  DF <- data.frame(row.names = name.dun, difference=difference, lower=lower, upper=upper, reject=reject)
 

  # grouping
  group <- vector("list",k)
  a=0
  for(i in 2:k){
    if(is.null(group[[i]])){
      a <- a+1
      for(j in k:i){
        dif <- sm[i-1]-sm[j]
        u <- dif+b.t*sqrt(MSE*(1/sn.i[i-1]+1/sn.i[j]))
        l <- dif-b.t*sqrt(MSE*(1/sn.i[i-1]+1/sn.i[j]))
        
        if(0>l&0<u){
          for(h in (i-1):j){
            group[[h]] <- paste(group[[h]],letters[a],sep="")
          }
          break
        }
        if(i==j){
          group[i-1] <- letters[a]
        }
      }
    }
  }
  if(is.null(group[[k]])){
    group[[k]] <- letters[a+1]
  }
  group.dat <- c()
  for(i in 1:k){
    group.dat[i] <- group[[i]]
  }
  group.dat <<- data.frame(sample=name.vec,group=group.dat)
 
  list(main="Bonferroni T Test",
       "Fit"=model$call,
       test=DF,
       group=group.dat)
}

bonferroni.func(y,x,alpha=0.05)
#pairwise.t.test(y,x)
# 1,3 has more data compared to 4,5

01

위의 사진을 보면 알 수 있듯이, 각 그룹별로 얼마정도의 차이를 근거로 같은 혹은 다른 그룹으로 분류한 건지 볼 수 있고,

그에 따른 그룹핑결과 또한 쉽게 확인해 볼 수 있습니다

---

# Scheffe

사실 위에서 진행한 Bonferroni 와 별반 다를것이 없는 프로그래밍입니다, 그렇기에 사진이나 세부설명은 넘기겠습니다

y <- c(1.51,1.92,1.08,2.04,2.14,1.76,1.17
       ,1.69,0.64,0.90,1.41,1.01,0.84,1.28,1.59
       ,1.56,1.22,1.32,1.39,1.33,1.54,1.04,2.25,1.49
       ,1.30,0.75,1.26,0.69,0.62,0.90,1.20,0.32
       ,0.73,0.80,0.90,1.24,0.82,0.72,0.57,1.18,0.54,1.30)
x <- as.factor(rep(1:5,c(7,8,9,8,10)))

sheffe.func <- function(y,x,alpha=0.05){
  n <- length(y); k <- nlevels(x); df <- n-k
  model <- aov(y~x)
  
  MSE <- deviance(model)/(n-k)
  
  mean.i <- tapply(y,x,mean)
  n.i <- tapply(y,x,length)
  
  raw.dat <- cbind(mean.i,n.i)
  
  sm <- raw.dat[order(mean.i),1]
  sn.i <- raw.dat[order(mean.i),2]
  
  name.vec <- as.numeric(names(sm))
  
  SHEFFE <- sqrt((k-1)*qf(1-alpha,k-1,n-k))
  
  reject <- upper <- lower  <- name.dun <- difference <- c()
  
  for(i in 1:(k-1)){
    for(j in k:2){
      if(j>i){
        dif <- sm[i]-sm[j]
        difference <- c(difference,abs(dif))
        name.dun <- c(name.dun,paste(name.vec[i],"-",name.vec[j],sep=""))
        u <- dif+SHEFFE*sqrt(MSE*(1/sn.i[i]+1/sn.i[j])); upper <- c(upper,u)
        l <- dif-SHEFFE*sqrt(MSE*(1/sn.i[i]+1/sn.i[j])); lower <- c(lower,l)
        reject <- c(reject,ifelse(0>l&0<u,"no","yes"))
      }
    }
  }

  DF <- data.frame(row.names = name.dun, difference=difference, lower=lower, upper=upper, reject=reject)
  
  # grouping
  group <- vector("list",k)
  a=0
  for(i in 2:k){
    if(is.null(group[[i]])){
      a <- a+1
      for(j in k:i){
        dif <- sm[i]-sm[j]
        u <- dif+SHEFFE*sqrt(MSE*(1/sn.i[i]+1/sn.i[j]))
        l <- dif-SHEFFE*sqrt(MSE*(1/sn.i[i]+1/sn.i[j]))
        
        if(0>l&0<u){
          for(h in (i-1):j){
            group[[h]] <- paste(group[[h]],letters[a],sep="")
          }
          break
        }
        if(i==j){
          group[i-1] <- letters[a]
        }
      }
    }
  }
  if(is.null(group[[k]])){
    group[[k]] <- letters[a+1]
  }
  group.dat <- c()
  for(i in 1:k){
    group.dat[i] <- group[[i]]
  }
  group.dat <- data.frame(sample=name.vec,group=group.dat)
  
  list(main="Scheffe Test",
       "Fit"=model$call,
       test=DF,
       group=group.dat)
}

sheffe.func(y,x,alpha=0.05)

---

# Duncan

위의 두 가지 사후검정과 조금 다른 식구성이 있지만, 딱히 어렵지 않은 구성이므로 빨강글씨로만 표기해두겠습니다

#duncan.test(model,"x",alpha=alpha,console=T)
library(pdftools)
library(stringr)

# use Duncan method (pg.527)
y <- c(1.51,1.92,1.08,2.04,2.14,1.76,1.17
       ,1.69,0.64,0.90,1.41,1.01,0.84,1.28,1.59
       ,1.56,1.22,1.32,1.39,1.33,1.54,1.04,2.25,1.49
       ,1.30,0.75,1.26,0.69,0.62,0.90,1.20,0.32
       ,0.73,0.80,0.90,1.24,0.82,0.72,0.57,1.18,0.54,1.30)
x <- as.factor(rep(1:5,c(7,8,9,8,10)))

model <- aov(y~x)

duncan.func <- function(y,x,alpha=0.05){
  dun <- readr::read_lines(pdf_text("https://www.york.ac.uk/depts/maths/histstat/tables/duncan.pdf"))

  dun.5 <- str_squish(dun[c(8:27,36:61)])
  
  dun.5 <- data.matrix(as.data.frame(do.call(rbind, strsplit(dun.5, split=" ")), stringsAsFactors=FALSE)[,-1])
  
  
  dun.1 <- str_squish(dun[c(71:90,99:124)])
  dun.1 <- data.matrix(as.data.frame(do.call(rbind, strsplit(dun.1, split=" ")), stringsAsFactors=FALSE)[,-1])
  
  
  # base data
  n <- length(y); k <- nlevels(x)
  model <- aov(y~x)
  
  MSE <- deviance(model)/(n-k)
  
  #sorting by mean
  mean.i <- tapply(y,x,mean)
  n.i <- tapply(y,x,length)
  
  raw.dat <- cbind(mean.i,n.i)
  raw.dat <- raw.dat[order(mean.i),]

  
  if(alpha==0.05){
    duncan <- dun.5
  } else if(alpha==0.01){
    duncan <- dun.1
    } else {stop("alpha must be 0.05 or 0.01")}
  
  df <- if(n-k>120){45} else if(n-k>80){44} else if(n-k>60){43} else if(n-k>40){41} else{n-k}
  
  r.p <- if(k<=12){
    duncan[df,1:(k-1)]
  } else if(k<=15){
      c(duncan[df,1:11],rep(duncan[df,12],k-12))
  } else if(k<=20){
      c(duncan[df,1:11],rep(duncan[df,12],3),rep(duncan[df,13],k-15))
    } else {stop("too many testing subjects")}
  
  SSR.p <- r.p*sqrt(MSE)
  
  # names of factors
  name.vec <- as.numeric(rownames(raw.dat))
  
  #  making matrix
  p <- reject <- len.dun  <- name.dun <- difference <- c()
  
  for(i in 1:(k-1)){
    for(j in k:2){
      if(i<j){
        dif <- raw.dat[j,1]-raw.dat[i,1]
        n1 <- raw.dat[j,2]
        n2 <- raw.dat[i,2]
        diff <- signif(dif*sqrt((2*n1*n2)/(n1+n2)),4)
        
        name.dun <- c(name.dun,paste(name.vec[i],"-",name.vec[j]),recursive=F)
        difference <- c(difference,diff)
        len.dun <- c(len.dun,signif(SSR.p[j-i],4))
        reject <- c(reject,ifelse(diff>SSR.p[j-i],"yes","no"))
        p <- c(p,j-i+1)
      }
    }
  }
  
  # grouping
  group <- vector("list",k)
  a=0
  for(i in 2:k){
    if(is.null(group[[i]])){
      a <- a+1
      for(j in k:i){
        dif <- raw.dat[j,1]-raw.dat[i-1,1]
        n1 <- raw.dat[j,2]
        n2 <- raw.dat[i,2]
        diff <- signif(dif*sqrt((2*n1*n2)/(n1+n2)),4)
        
        if(diff<SSR.p[j-i+1]){
          for(h in (i-1):j){
            group[[h]] <- paste(group[[h]],letters[a],sep="")
          }
          break
        }
        if(i==j){
          group[i-1] <- letters[a]
        }
      }
    }
  }
  if(is.null(group[[k]])){
    group[[k]] <- letters[a+1]
  }
  group.dat <- c()
  for(i in 1:k){
    group.dat[i] <- group[[i]]
  }
  group.dat <- data.frame(sample=name.vec,group=group.dat)

  DF <- data.frame(p=p,"test statistic"=difference,SSR.p=len.dun,"reject H0"=reject,row.names=name.dun)

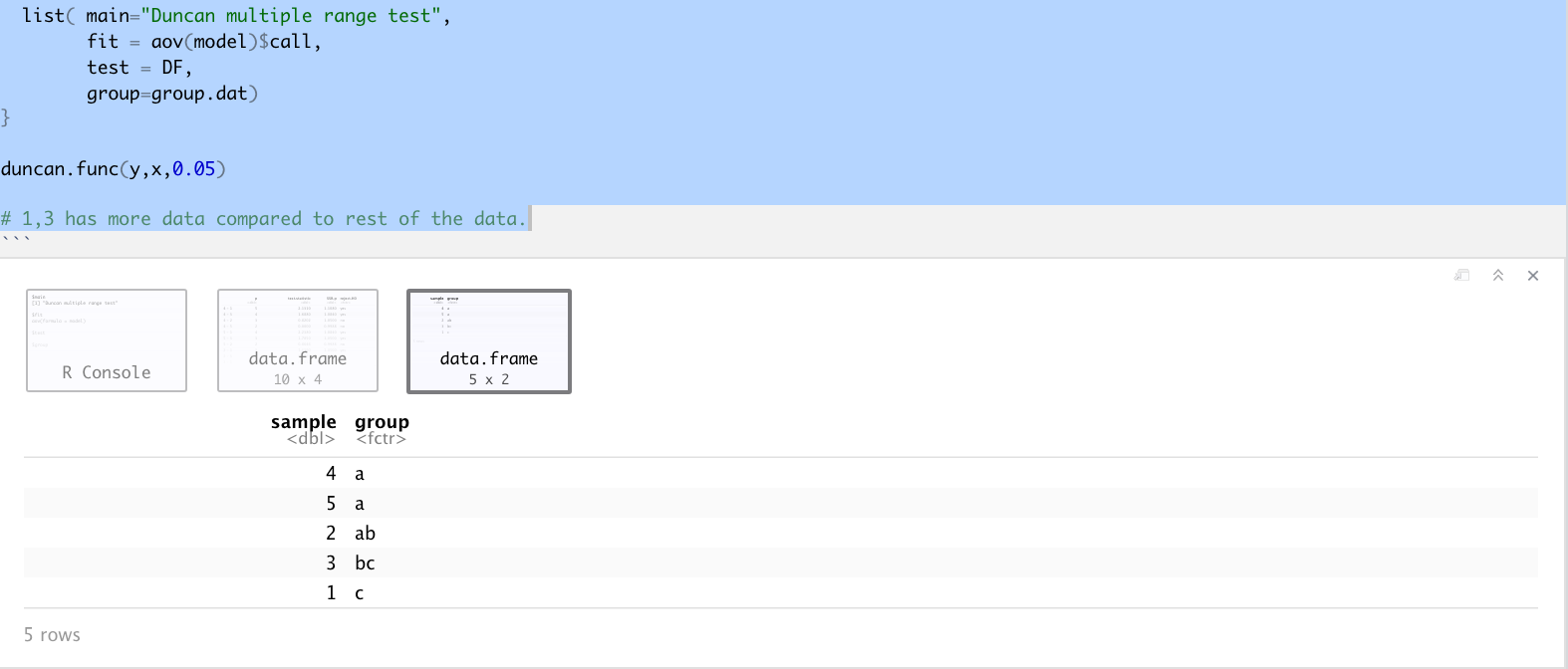
  list( main="Duncan multiple range test",
        fit = aov(model)$call,
        test = DF,
        group=group.dat)
}

duncan.func(y,x,0.05)

# 1,3 has more data compared to rest of the data.

01