미적분학 2-1. 매개방정식과 극좌표로 나타낸 곡선의 그래프

1. 매개방정식과 극좌표로 나타낸 곡선의 그래프

plot( x(t), y(t), t=range of t], option) : 매개방정식

plot( r(t), t, t=range of t], coords=polar) : 극좌표

 

---

예제

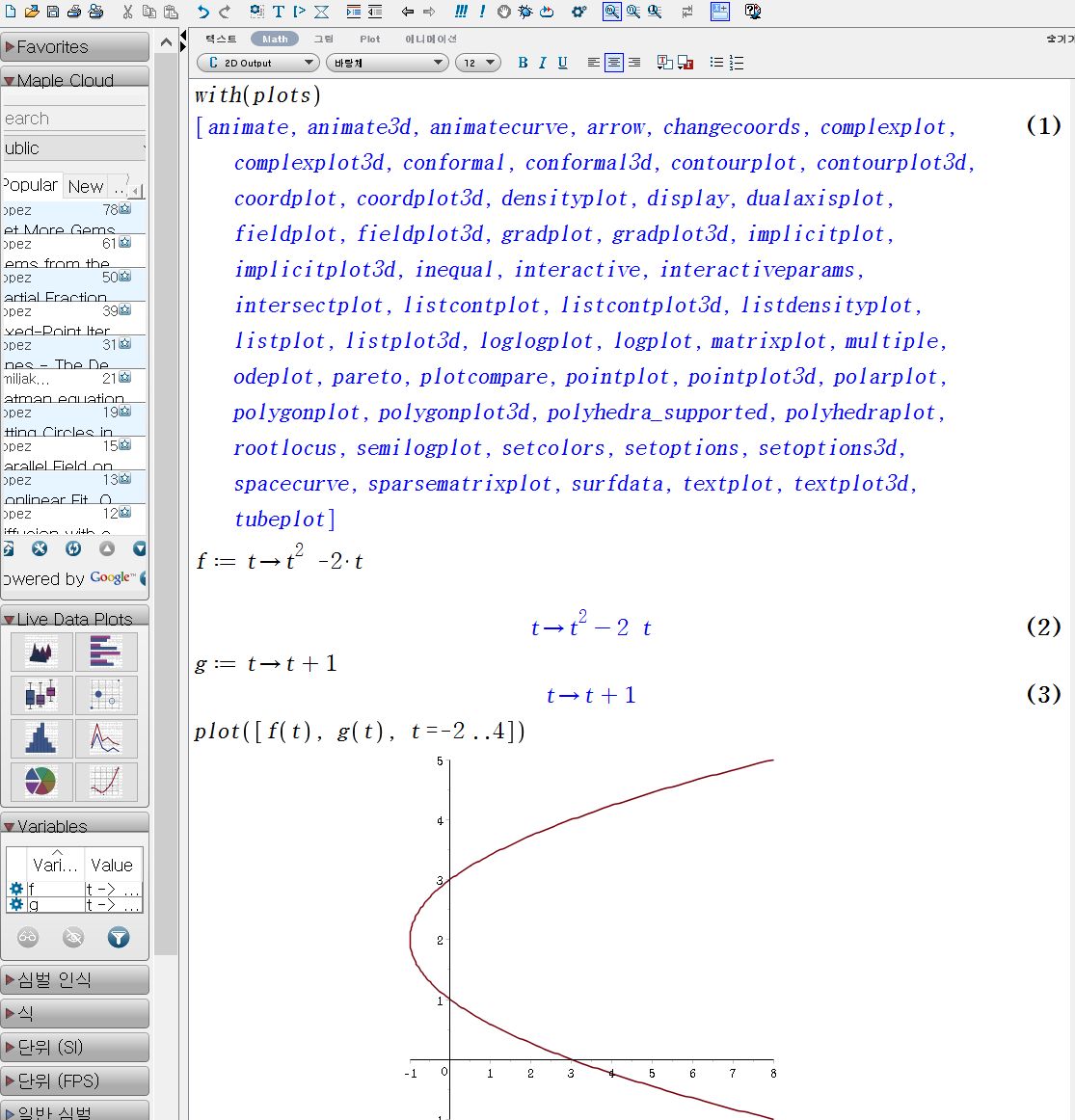
매개변수방정식 "x=t^2 -2t, y=t+1" 로 정의되는 곡선의 개형을 그리고 확인하여라.

 

with(plots)

f:=t->t^2 -2*t

g:=t->t+1

plot([f(t), g(t), t=-2..4])

---

예제

곡선 C가 매개변수방정식 "x=t^2, y=t^3-3t" 로 정의될 때,
(a). C가 점 (3,0)에서 두 개의 접선을 가짐을 보이고 그 방정식을 구하여라
(b). C 위에서 수평접선 또는 수직접선을 가지는 점을 찾아라
(c). 이 곡선이 어디에서 위로 오목 또는 아래로 오목한가를 결정하여라
(d). 곡선의 개형을 그려라

 

with(plots)

f:=t->t^2

g:=t->t^3 -3*t

df:=diff(f(t), t)

dg:=diff(g(t), t)

dy:=dg/df

tval:=solve(f(t)=3,t)

l1:=subs(t=tval[1], dy) *(x-3)

l2:=subs(t=tval[2], dy) *(x-3)

p1:=plot(l1, x=-1..5, y=-4..4, color=blue)

p2:=plot(l2, x=-1..5, y=-4..4, color=green)

p3:=plot([f(t), g(t), t=-2..2])

display({p1,p2,p3})

---

예제

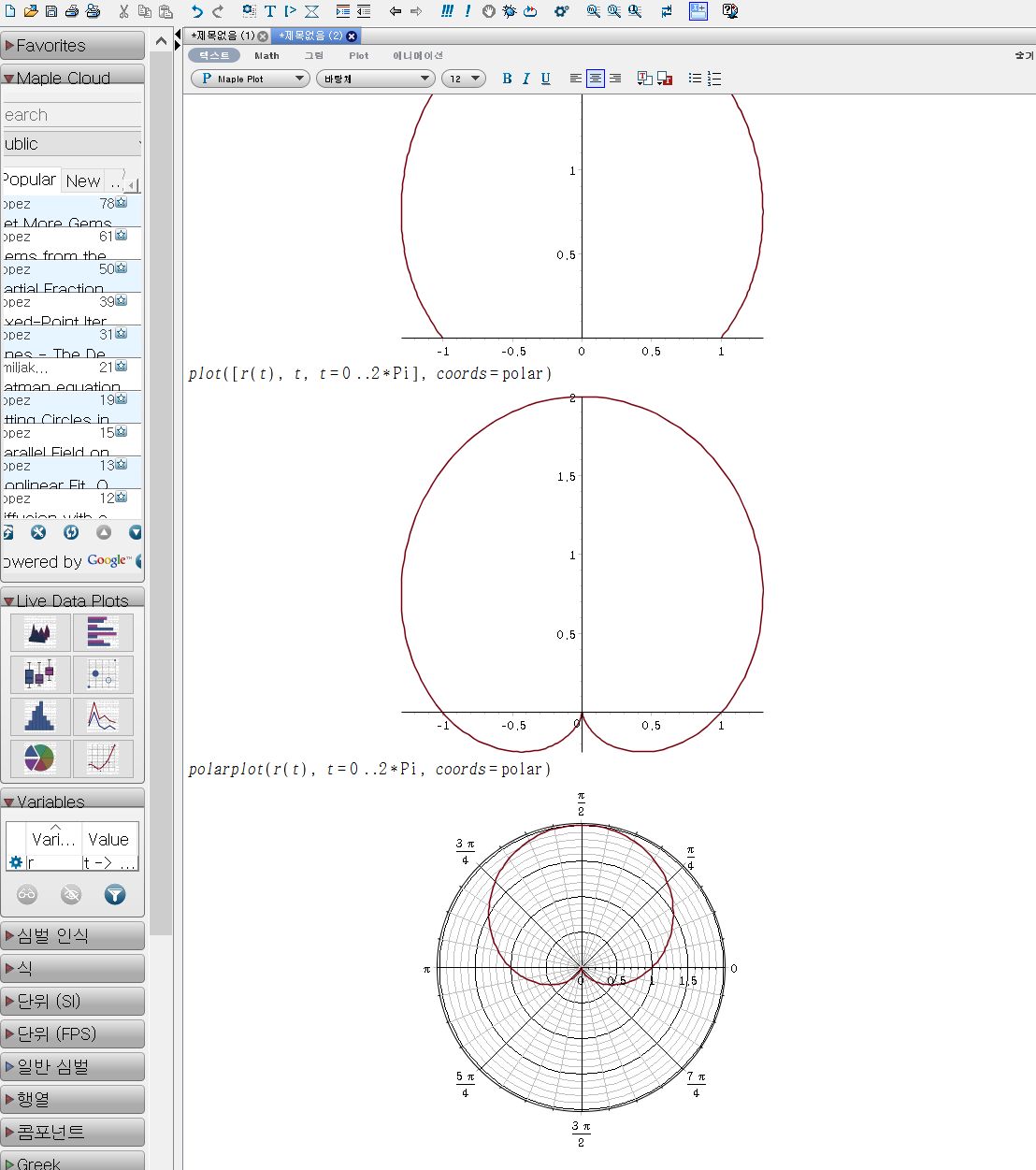
곡선 r=1+sinΘ 의 개형을 그려라.

 

with(plots)

r:=t->1+sin(t)

plot([r(t), t, t=0..Pi], coords=polar)

plot([r(t), t, t=0..2*Pi], coords=polar)

polarplot(r(t), t=0..2*Pi, coords=polar)

---

예제

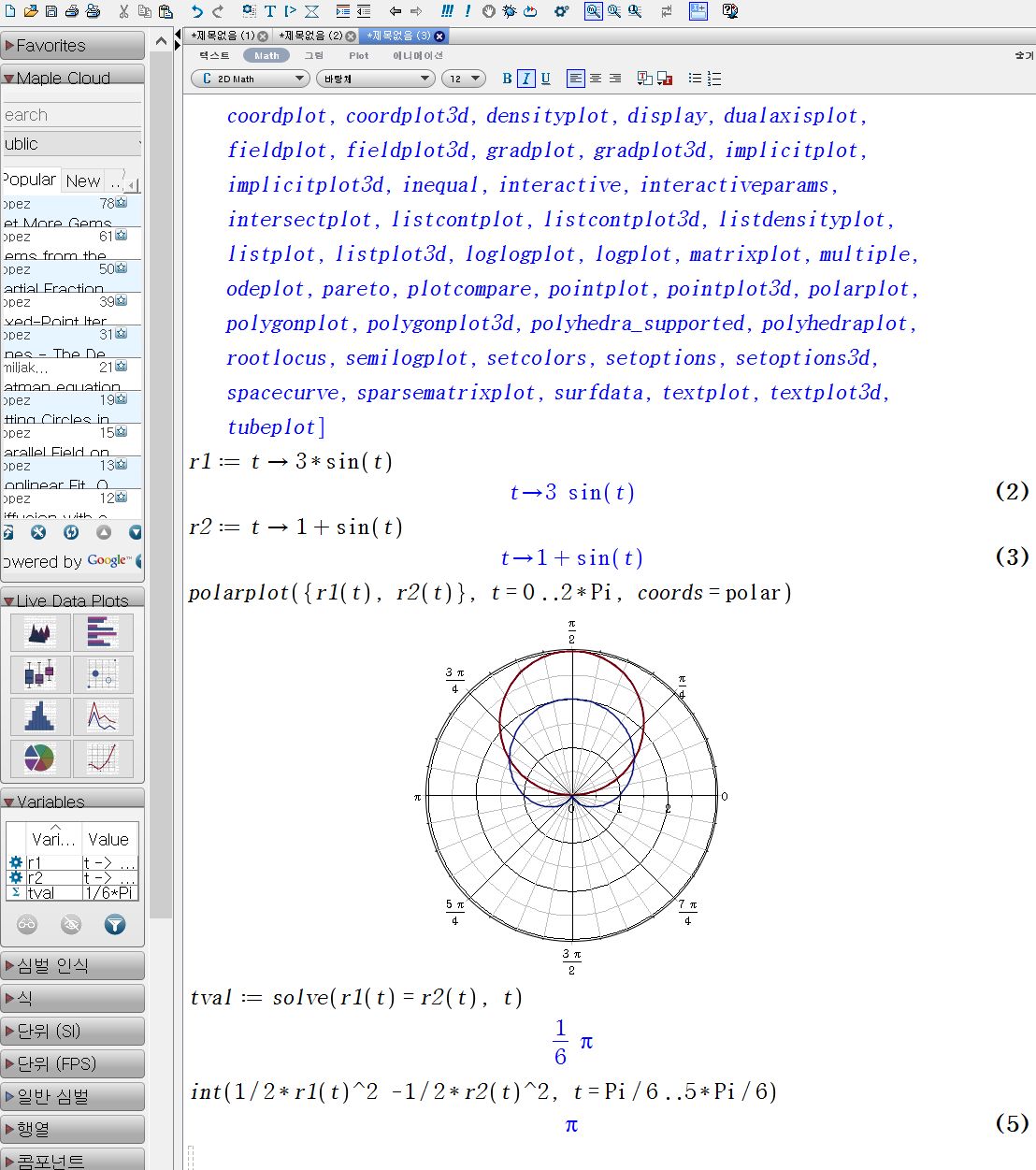
원 r=3sinΘ의 내부와 심장형 r=1+sinΘ의 외부에 놓인 영역의 넓이를 구하여라.

 

with(plots)

r1:=t->3*sin(t)

r2:=t->1+sin(t)

polarplot({r1(t), r2(t)}, t=0..2*Pi, coords=polar)

tval:=solve(r1(t)=r2(t), t)

int(1/2*r1(t)^2 -1/2*r2(t)^2, t=Pi/6..5*Pi/6)

---

직접해보기

(a). 곡선의 직교좌표 방정식을 구하기 위하여 매개변수를 소거하여라
(b). 곡선의 개형을 그리고 매개변수가 증가함에 따라 추적되는 곡선의 방향을 화살표로 나타내어라

x=sin(1/2)Θ,   y=cos(1/2)Θ,   -π<= Θ <=π

 

직교좌표에 Θ의 함수로서 r을 먼저 그림으로써, 극방정식으로 주어진 곡선의 개형을 그려라.

r=-2sinΘ